Post by ChrisK on Mar 26, 2008 14:09:33 GMT -5
(Note: sumgai has pointed out the I have a "D" instead of a "C" in the column under header "1 of 3" on all of the charts. He's right, but it's way more than somewhat unlikely that I'm gonna change them anytime soon since it's not related to the theme.) 
Lazy is.
When you wire up that new scheme or are simply trying to decipher an existing one and it doesn't work, what does one do.
One could post for help on this board (still highly recommended) and hope that someone has had a similar problem or can figure out what is amiss, or one could first apply some deductive reasoning.
Now, I always recommend that one measure and write down the resistance of each pot and pickup used in any guitar for WHEN one has to support things when issues arise.
One can use such values, either recorded or discerned one way or another to decipher what is going on inside the guitar. Here's a result of these processes on a guitar with non-standard (non-regular) Strat wiring. (Scroll down, look at the shiny pictures and scroll down some more.)
While these procedures can be used to discern what is amiss and amok, meaningful data require fairly resolute (and accurate) multi-meters for best results.
If the pickups are substituted with resistors until the wiring is checked out, any issues become fairly obvious. One has to choose the resistor values carefully for best results (well, the EEs amongst us well know that it's a 1/2/4 ratio). I recommend that equal value resistors be used such as 10K Ohms. If two are in parallel, 5K results and if two are in series, 20K results. One alone is, well, 10 K. this is a 1/2/4 ratio. Since resistors often come in packs of 5.......................
Let's evaluate the results for the 17 possible combinations of three coils sans phase and none/off. All results are coerced to the values that will appear on a 3 1/2 digit multi-meter (0 to 1999). Please note that while the columns on the left indicate the semi-standard method of representing pickup combinations ("+" is parallel, "*" is series), the column labeled "Math" is just that; the equation mathematics for value derivation.
When two resistances are in parallel, one calculates this by R = A * B/ or R = 1/[1/A + 1/B] (which nicely scales for "n" values R = 1/[1/A + 1/B + ........+ 1/n].
When two resistances are in series, one just adds the values R = A + B
Not using such a 1/2/4 ratio can be problematic. Here is an example with a reasonable ratio of pickup values. Dang, there are common results for more than one combination.
i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations5_7-5_1020080307.jpg
Let's change it a little. Uh oh, there are again common results for more than one combination.
i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations6_10_1520080307.jpg
What happens when there are two pickups with the same value? Dang^2i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations5_5_620080307.jpg
How about for all three being the same value? Dang^3
i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations5_5_520080307.jpg
So, what about the 1/2/4 solution? (we'll use 5/10/20 since these are in the general range of guitar pickups and 10K resistors are most common.)
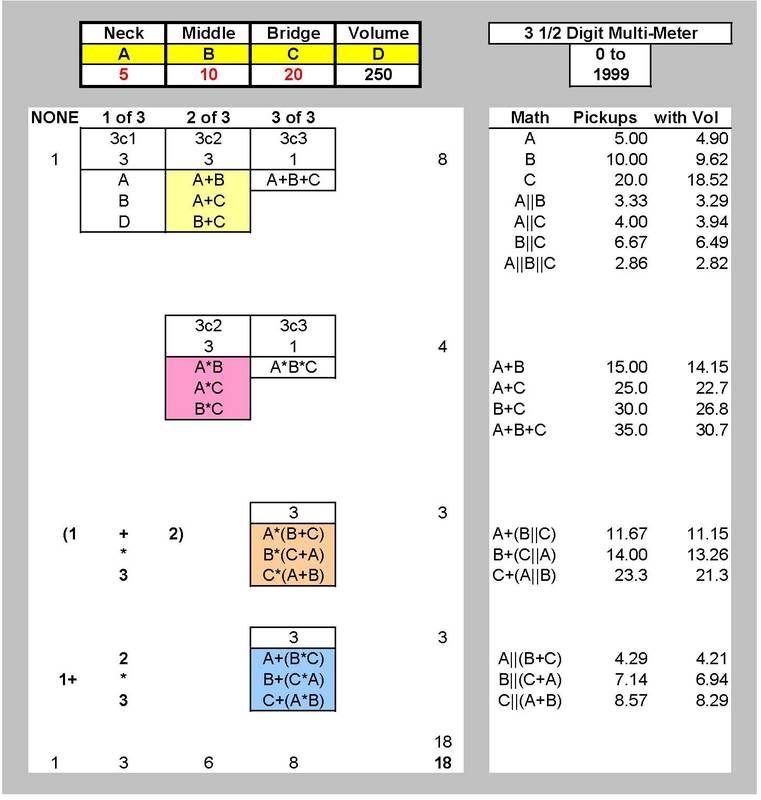
(Excursions caused by the use of zero and infinity are less than well contained in non-symbolic math.)
Let's look at the results for a shorted bridge pickup (0.000001 means 0.000001 K ohms or 0.001 Ohms). We can see that shorts are quite dominant in the parallel combinations.

Let's look at the results for an open neck pickup (100,000 means 100,000 K Ohms). We can see that opens are quite dominant in the series combinations.
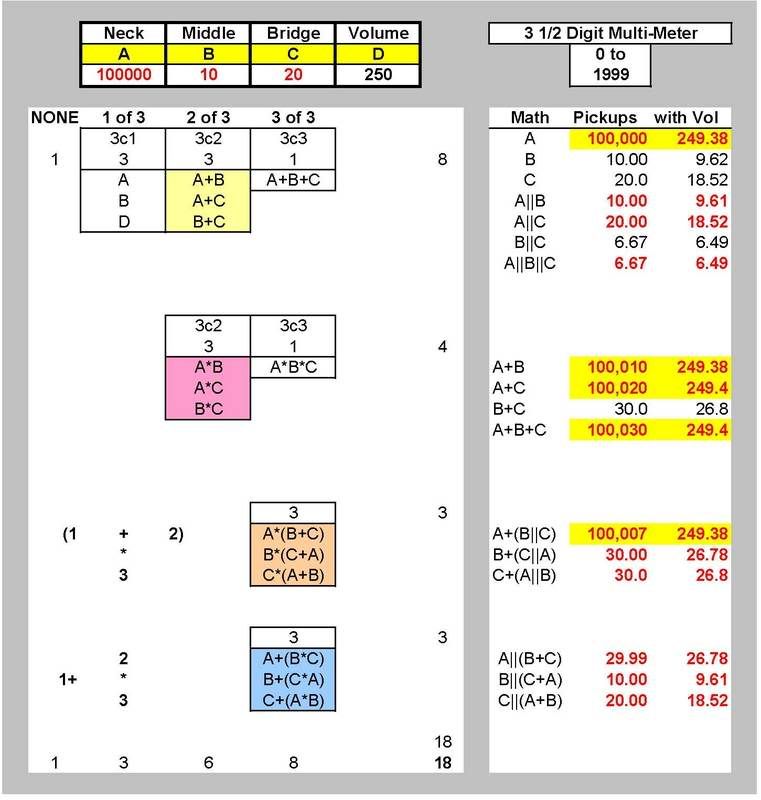
While the pickup (and resistor) may well not be shorted itself, this will give clues as to where in the wiring the fault lies.
I use this method by installing the resistors and checking my own wiring empirically before wiring in the actual pickups. I check phase combinations by using the pickups and my ears once I know that the wiring is non-GeFooey.

Lazy is.
When you wire up that new scheme or are simply trying to decipher an existing one and it doesn't work, what does one do.
One could post for help on this board (still highly recommended) and hope that someone has had a similar problem or can figure out what is amiss, or one could first apply some deductive reasoning.
Now, I always recommend that one measure and write down the resistance of each pot and pickup used in any guitar for WHEN one has to support things when issues arise.
One can use such values, either recorded or discerned one way or another to decipher what is going on inside the guitar. Here's a result of these processes on a guitar with non-standard (non-regular) Strat wiring. (Scroll down, look at the shiny pictures and scroll down some more.)
While these procedures can be used to discern what is amiss and amok, meaningful data require fairly resolute (and accurate) multi-meters for best results.
If the pickups are substituted with resistors until the wiring is checked out, any issues become fairly obvious. One has to choose the resistor values carefully for best results (well, the EEs amongst us well know that it's a 1/2/4 ratio). I recommend that equal value resistors be used such as 10K Ohms. If two are in parallel, 5K results and if two are in series, 20K results. One alone is, well, 10 K. this is a 1/2/4 ratio. Since resistors often come in packs of 5.......................
Let's evaluate the results for the 17 possible combinations of three coils sans phase and none/off. All results are coerced to the values that will appear on a 3 1/2 digit multi-meter (0 to 1999). Please note that while the columns on the left indicate the semi-standard method of representing pickup combinations ("+" is parallel, "*" is series), the column labeled "Math" is just that; the equation mathematics for value derivation.
When two resistances are in parallel, one calculates this by R = A * B/ or R = 1/[1/A + 1/B] (which nicely scales for "n" values R = 1/[1/A + 1/B + ........+ 1/n].
When two resistances are in series, one just adds the values R = A + B
Not using such a 1/2/4 ratio can be problematic. Here is an example with a reasonable ratio of pickup values. Dang, there are common results for more than one combination.
i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations5_7-5_1020080307.jpg
Let's change it a little. Uh oh, there are again common results for more than one combination.
i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations6_10_1520080307.jpg
What happens when there are two pickups with the same value? Dang^2i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations5_5_620080307.jpg
How about for all three being the same value? Dang^3
i37.photobucket.com/albums/e84/cekikta/Wiring/Testing%20Wiring/PickupCombinations5_5_520080307.jpg
So, what about the 1/2/4 solution? (we'll use 5/10/20 since these are in the general range of guitar pickups and 10K resistors are most common.)


(Excursions caused by the use of zero and infinity are less than well contained in non-symbolic math.)
Let's look at the results for a shorted bridge pickup (0.000001 means 0.000001 K ohms or 0.001 Ohms). We can see that shorts are quite dominant in the parallel combinations.

Let's look at the results for an open neck pickup (100,000 means 100,000 K Ohms). We can see that opens are quite dominant in the series combinations.

While the pickup (and resistor) may well not be shorted itself, this will give clues as to where in the wiring the fault lies.
I use this method by installing the resistors and checking my own wiring empirically before wiring in the actual pickups. I check phase combinations by using the pickups and my ears once I know that the wiring is non-GeFooey.



