|
|
Post by antigua on Jan 6, 2018 11:02:13 GMT -5
Reducing coil capacitance is a big deal in pickup design, because capacitance plus inductance reduce the treble response of a pickup, so if capacitance can be reduced, inductance can be raised and the pickup will become louder. I cam across some interesting insights here: coefs.uncc.edu/mnoras/files/2013/03/Transformer-and-Inductor-Design-Handbook_Chapter_17.pdf It seems that increasing the wire insulation thickness, or getting an insulation with a lower dielectric constant, should decrease the "winding capacitance", just as it's stated above. As for the "leakage inductance", as I understand it, this is only a concern in the context of a transformer, where you want one coil to magnetically coupling tightly with another. If "leakage inductance" is an issue with inductors, or guitar pickups, it's a much, much smaller issue. Guitar pickups and guitar strings sort of relate like a transformer, in fact, but the magnetic coupling between the pickup and the guitar string is so weak and inefficient that a pickup is much more an inductor and much less a transformer. When it comes to general inductor design, it appears the main reason they'd want to use a thinner insulation is just to reduce the size of the coil. If a coil caries a low voltage and operates at a low temperature, it's mostly just the case that thick insulation is not a requirement, but it might still be advantageous from a parasitic capacitance standpoint. Most pickup designs out there usually have some room to spare, so I'm not sure why a pickup maker wouldn't want the thickest insulation with the lower dielectric constant they can find. As for the layer to layer capacitance, it says that if the wire is laid in a "fold back" pattern that you get a lower voltage gradient, because where you have two wires side by side, this would ensure that there is a minimal amount of copper wire length between them, less wire length means lower voltage gradient. If a CNC pickup winder could be configured to wind a pickup with this "foldback" method, it might well produce a pickup with a higher inductance to a lower capacitance. I had another thread a while back guitarnuts2.proboards.com/thread/7888/parasitic-capacitance-associated-magnetic-axis looking at the issue of coil capacitance with respect to the axis of the coil. Some person or persons has made a case that if magnetic fields relate along the long axis, then the electric force that constitutes the capacitive dynamic must only relate perpendicular to the magnetic axis.. because of the right hand rule, magnetic field goes this way, electric field goes that way. If true, it supports the concept of "foldback winding", because it means that you'd want to reduce the wire length between one winding and the next. Whatever the case may be, the less "circuit" distance there is between physically close conductors, the lower the voltage gradient. |
|
|
|
Post by reTrEaD on Jan 6, 2018 11:38:38 GMT -5
As for the layer to layer capacitance, it says that if the wire is laid in a "fold back" pattern that you get a lower voltage gradient, because where you have two wires side by side, this would ensure that there is a minimal amount of copper wire length between them, less wire length means lower voltage gradient. I'm having a difficult time wrapping my mind around this. If we look at the relationship of the capacitances that exist between two layers, it seems like the foldback winding technique would result in a consistent length of wire between each of the 'capacitors'. It's true that in the U winding technique that the beginning of one winding and the end of the next winding would have roughly twice as much length of wire between the 'capacitors' at that end. But at the end where the middle of the U occurs, there would be a very short length of wire between those 'capacitors'. It seems like each and every one of the many 'capacitors' in the foldback wind would theoretically have a wire length of 1 between them. The capacitors in the U wind would have wire lengths between them that vary from nearly zero to a maximum of 2. I must be missing something. It seems like the net result should be equal. |
|
|
|
Post by reTrEaD on Jan 6, 2018 13:20:33 GMT -5
I must be missing something. After this rattled around in my head for a while, I think I discovered my fatal flaw. I was visualizing a string of capacitors and placing varying resistances between them. I should have been thinking of a string of resistances with capacitors placed between varying points in that string.  Each resistor represents half of the total length of one wind winding layer. Only three capacitors are shown but I think they do a reasonable job of displaying how the result is very different between the two winding techniques. |
|
|
|
Post by ms on Jan 6, 2018 15:20:44 GMT -5
But then there is the cable capacitance, which is more that the coil capacitance. This puts a limit on how much you can improve things in a passive circuit.
If you really need some combination of more output, more signal to noise, and more high frequency response, you use an on board preamp. Then you can have essentially anything you want.
|
|
|
|
Post by antigua on Jan 6, 2018 15:44:58 GMT -5
I must be missing something. After this rattled around in my head for a while, I think I discovered my fatal flaw. I was visualizing a string of capacitors and placing varying resistances between them. I should have been thinking of a string of resistances with capacitors placed between varying points in that string.  Each resistor represents half of the total length of one wind. Only three capacitors are shown but I think they do a reasonable job of displaying how the result is very different between the two winding techniques. I'm having a hard time wrapping my head around it. I agreed with your first assessment, it seems like you would end up with the same average, like the difference between 2+2+2+2 versus 1+3+1+3, but the theoretical topography of the "capacitors" is complicated and would put some in series and other in parallel. I have to admit, I think I trust this source a little too much because it was printed in an actual book with paper, and the PDF is hosted by a University, but I went googling to find out more about "foldback technique" and I don't see other mentions of it outside of this author, and maybe one other. Maybe there is another term for it, but this shakes my confidence in the concept. I have seen this "coil winding voltage gradient" issue in another context, though, tapped coils such as the SSL-5 guitarnuts2.proboards.com/thread/8022/seymour-duncan-ssl-analysis-review . When you have an unused chuck right beside the primary winding that is in circuit at one end, the capacitive coupling between the unused coil and primary is higher than the capacitance you get when both coils are in circuit. Full capacitance 131pF, tapped capacitance is 463pF, based on the resonant peak in relation to the inductance. So just by rearranging where the wire is in circuit, you can wildy alter the capacitance, but surely any difference in winding pattern would be a small fraction of what is seen in the tapped coil example. The part about using thicker insulator seems pretty sound, though. As of this moment, I don't know why pickup makers don't always favor heavy build wire. |
|
|
|
Post by antigua on Jan 6, 2018 15:55:18 GMT -5
But then there is the cable capacitance, which is more that the coil capacitance. This puts a limit on how much you can improve things in a passive circuit. If you really need some combination of more output, more signal to noise, and more high frequency response, you use an on board preamp. Then you can have essentially anything you want. Regarding a preamp, when it comes to pickup design, there is sort of a game being played. The game is impact as much as you can with just coil(s), magnets and structural part and shielding. Pre amps and zero capacitance guitar cables and other battery operated solutions actually solve most if not all the "problems", but it's like bringing a gun to an archery competition. There's still a market of pickup makers out there promising to improve on the old passive design. They sell pickups that ship out in little boxes, meant to be drop in replacements and not whole new wiring harnesses, like the new Fishman powered pickups, so the limitations are both real and imagined. Usually they don't really improve anything, either because that was never their intent, or they don't understand the thing they're trying to improve. They will try things like lower resistance magnet wire, or promise that inert materials somehow benefit the tone. It's hard to tell if they're BS'ing customers or if they honestly believe it, either way we have an information deficit. And so the point of this exercise to optimize the thing as much as possible given a fixed set of boundaries. 10pF less capacitance might be peanuts, but it's an honest improvement, if achieved. |
|
|
|
Post by reTrEaD on Jan 6, 2018 18:21:00 GMT -5
I'm having a hard time wrapping my head around it. I agreed with your first assessment, it seems like you would end up with the same average, like the difference between 2+2+2+2 versus 1+3+1+3, but the theoretical topography of the "capacitors" is complicated and would put some in series and other in parallel. My first drawing wasn't labeled and my explanation for the resistors wasn't quite right. I should have said each resistor represents 1/2 of the length of a winding layer. We could think of a very long series chain with each individual wind as a tiny source, small inductance, and small resistance in series. We have inter-layer capacitances that exist but the winding pattern dictates where each one of the tiny capacitors connect. My intent was to show just three of those capacitors, although there are a huge number of them between any two layers. C1 represents the capacitance between the very first turn of the first layer and the nearest turn on the second layer. C2 represents the capacitance between the turn at the midpoint of the first layer and the nearest turn on the second layer. C3 represents the capacitance between the very turn winding on the first layer and the nearest turn on the second layer.  C2 (the midpoint of each winding layer) hasn't changed its connection points regardless of winding technique. C1 and C3 have radically different connections within the chain, depending on the winding technique. The size of C3 in the U-type winding is still the same but it connects from the last turn of layer-1 to the first turn of layer-1. They are adjacent in the series chain. Its effect has been reduced to near zero. The size of C1 in the U-type winding is still the same but it connects from the very first turn of the two-layer chain to the very last turn. They are at extreme ends of the series chain. I would expect the effect of C1 on the two-layer total to be very great, in the U-type winding. Far greater than 2x C2's effect. In my (admittedly coarse) estimation, in the U-type winding we gain far more effect of the capacitance at C1 than we lost at C3. |
|
Deleted
Deleted Member
Posts: 0
Likes:
|
Post by Deleted on Jan 7, 2018 6:59:07 GMT -5
Antigua, you are doing a greak work here. I highly appreciate your methods and philosophy. You definitely are the person to consult about anything pups-related (and not restricted to pups only).
I am wondering if you are doing this as a hobby, as academic research, or professionally.
|
|
|
|
Post by antigua on Jan 7, 2018 12:11:17 GMT -5
Antigua, you are doing a greak work here. I highly appreciate your methods and philosophy. You definitely are the person to consult about anything pups-related (and not restricted to pups only).
I am wondering if you are doing this as a hobby, as academic research, or professionally.Thanks, there are people who know much more than I do when it comes to the actual science, physics and math, and especially the minutia of pickup making history, though I'd also say such people are often not available, and the war on facts that is being propagated in the major guitar forums easily eclipses those people's energies, which is why I feel compelled to do this. I do this as a hobby. I probably have Aspergers, though I've never been diagnosed. My loss is hopefully your gain. When it comes to things like "what coil winding yields the lowest parasitic capacitance?", I'm really shocked that it's 2018 and all you can find on the Internet is bits and scraps of information, but on the other hand we have self driving electric cars, too. It's like in some respects things are futuristic, and in others they're horse and buggy. |
|
|
|
Post by antigua on Jan 7, 2018 15:49:36 GMT -5
I'm having a hard time wrapping my head around it. I agreed with your first assessment, it seems like you would end up with the same average, like the difference between 2+2+2+2 versus 1+3+1+3, but the theoretical topography of the "capacitors" is complicated and would put some in series and other in parallel. My first drawing wasn't labeled and my explanation for the resistors wasn't quite right. I should have said each resistor represents 1/2 of the length of a winding layer. We could think of a very long series chain with each individual wind as a tiny source, small inductance, and small resistance in series. We have inter-layer capacitances that exist but the winding pattern dictates where each one of the tiny capacitors connect. My intent was to show just three of those capacitors, although there are a huge number of them between any two layers. C1 represents the capacitance between the very first turn of the first layer and the nearest turn on the second layer. C2 represents the capacitance between the turn at the midpoint of the first layer and the nearest turn on the second layer. C3 represents the capacitance between the very turn winding on the first layer and the nearest turn on the second layer.  C2 (the midpoint of each winding layer) hasn't changed its connection points regardless of winding technique. C1 and C3 have radically different connections within the chain, depending on the winding technique. The size of C3 in the U-type winding is still the same but it connects from the last turn of layer-1 to the first turn of layer-1. They are adjacent in the series chain. Its effect has been reduced to near zero. The size of C1 in the U-type winding is still the same but it connects from the very first turn of the two-layer chain to the very last turn. They are at extreme ends of the series chain. I would expect the effect of C1 on the two-layer total to be very great, in the U-type winding. Far greater than 2x C2's effect. In my (admittedly coarse) estimation, in the U-type winding we gain far more effect of the capacitance at C1 than we lost at C3. This seems like a reasonable analysis, assuming the modeling is correct. I tried it out in LTSpice, which is my version of a cheat calculator since I'm not strong on the math, and for x = C1 = C2 = C3 , the foldback model does result in a higher resonant peak. With so few sources covering the subject, we don't know if this foldback vs. u-wind business tried and true truth, or just theoretical speculation on the part of Colonel Wm. T. McLyman, who is apparently the author . His writing is worded in a way that makes it sound like more than just a guess "The foldback winding technique, shown in Figure 17-14, is preferred to the normal U type winding, even though it takes an extra step before starting the next layer", preferred by who, under what circumstances? I guess there just isn't enough of a need for minimal capacitance coils to warrant the research, even though it seems like a rather fundamental aspects of physics which shouldn't be too difficult for trained professionals to work and and unravel. Maybe some day I will have a CNC winder I can use to make extremely specific coil windings, but that's a ways off. |
|
Deleted
Deleted Member
Posts: 0
Likes:
|
Post by Deleted on Jan 7, 2018 15:52:33 GMT -5
Antigua, you are doing a greak work here. I highly appreciate your methods and philosophy. You definitely are the person to consult about anything pups-related (and not restricted to pups only).
I am wondering if you are doing this as a hobby, as academic research, or professionally.Thanks, there are people who know much more than I do when it comes to the actual science, physics and math, and especially the minutia of pickup making history, though I'd also say such people are often not available, and the war on facts that is being propagated in the major guitar forums easily eclipses those people's energies, which is why I feel compelled to do this. I do this as a hobby. I probably have Aspergers, though I've never been diagnosed. My loss is hopefully your gain. When it comes to things like "what coil winding yields the lowest parasitic capacitance?", I'm really shocked that it's 2018 and all you can find on the Internet is bits and scraps of information, but on the other hand we have self driving electric cars, too. It's like in some respects things are futuristic, and in others they're horse and buggy. Aspergers ? Just googled it, does not seem anything too abnormal. I totally agree in what you say about quantum computing of 21 century vs caps/resistors/pups/analog tech of the 40s. I'll tell you my thought. Guitars and their technology are today a thing of the elite who runs this world. Clinton posing with Jimmy Page?? WTF? Those guys who are now 50-70 most probably were hippies some time in 1960-1980. Those guys like to live their dream as if when they were young. That's why guitars are so much coupled as a fetish with vintage tech. That's why rock'n'roll, although effectively gone and dead, is still so much politically correct. Elite loves it, cause it has been a successful instrument of so much control upon the youths of this world for so many years back. How many (orange) "revolutions" were started by some rolling stones or U2 concert... That's why we see ads of guitars, ppl playing guitars everywhere *BUT* in reality, young kids DONT like guitars, this music is not popular any more. |
|
|
|
Post by antigua on Jan 7, 2018 17:02:20 GMT -5
Aspergers ? Just googled it, does not seem anything too abnormal. It's not a big deal, but people think I must have a financial stake in guitar pickups to be doing this, I don't think they appreciate that some people can be very dedicated to specific things. I totally agree in what you say about quantum computing of 21 century vs caps/resistors/pups/analog tech of the 40s. I'll tell you my thought. Guitars and their technology are today a thing of the elite who runs this world. Clinton posing with Jimmy Page?? WTF? Those guys who are now 50-70 most probably were hippies some time in 1960-1980. Those guys like to live their dream as if when they were young. That's why guitars are so much coupled as a fetish with vintage tech. That's why rock'n'roll, although effectively gone and dead, is still so much politically correct. Elite loves it, cause it has been a successful instrument of so much control upon the youths of this world for so many years back. How many (orange) "revolutions" were started by some rolling stones or U2 concert... That's why we see ads of guitars, ppl playing guitars everywhere *BUT* in reality, young kids DONT like guitars, this music is not popular any more. I don't follow exactly, but I'll tell you that new guitar based music is still highly marketable, but not only that, there's always renewed interest in heroes of the past, like Jimi Hendrix, Beatles, David Bowie, because we live in a day and age where society no longer elevates anyone to such a mythical status, and because music was one of the few staple forms of entertainment at the time, they put a lot of effort into their craft, relative to today, where most music is mostly composed of production magic, style over substance. A given piece of music doesn't generate as much money, so it has to be created for less money. existence of an ever growing back catalog just further depresses the value of new content. I think the real difference is that, in the 60-70s, there was a push to try new things, such as the Alembic guitars with a dozen switches and built in pre amps, but all of that failed to catch on, and by the 80's, everyone went nuts for high output pickups and Floyd Rose trems, but by the 90's, and ever since, people either want stock guitars, or 50's vintage guitars. There no longer much interest in experimentation, nor heavy modding, and so that keeps guitarists from taking too great an interest in the finer workings of pickups. They're interested in the dimensionless quantity of mojo, and little else. |
|
|
|
Post by reTrEaD on Jan 8, 2018 14:06:33 GMT -5
With so few sources covering the subject, we don't know if this foldback vs. u-wind business tried and true truth, or just theoretical speculation on the part of Colonel Wm. T. McLyman, who is apparently the author . His writing is worded in a way that makes it sound like more than just a guess "The foldback winding technique, shown in Figure 17-14, is preferred to the normal U type winding, even though it takes an extra step before starting the next layer", preferred by who, under what circumstances? Yes, you closed with two interesting questions. I googled the italicized phrase and indeed it (and the drawing) came from a book by McLyman. I also found an "about the author" bio on him. If you're curious: kgmagnetics.com/?q=node/3I also stumbled across another, somewhat related technique called bank winding. It probably applies best to situations where the number of layers would be fewer than the number of turns in a layer (tall bobbin). Sheet 10 of this PDF. www.ti.com/lit/ml/slup125/slup125.pdf |
|
|
|
Post by antigua on Jan 9, 2018 21:55:15 GMT -5
With so few sources covering the subject, we don't know if this foldback vs. u-wind business tried and true truth, or just theoretical speculation on the part of Colonel Wm. T. McLyman, who is apparently the author . His writing is worded in a way that makes it sound like more than just a guess "The foldback winding technique, shown in Figure 17-14, is preferred to the normal U type winding, even though it takes an extra step before starting the next layer", preferred by who, under what circumstances? Yes, you closed with two interesting questions. I googled the italicized phrase and indeed it (and the drawing) came from a book by McLyman. I also found an "about the author" bio on him. If you're curious: kgmagnetics.com/?q=node/3I also stumbled across another, somewhat related technique called bank winding. It probably applies best to situations where the number of layers would be fewer than the number of turns in a layer (tall bobbin). Sheet 10 of this PDF. www.ti.com/lit/ml/slup125/slup125.pdfI see that Colonel Wm. T. McLyman is 85 years old. So on the one hand the window of opportunity to contact him and ask questions will close fast, but on the other, I don't think an 85 year old wants to deal with this stuff, and he wrote that book exactly 30 years ago now. That other PDF is very interesting, I'm still slogging through it. There was an interesting bit: "The basic rule governing the current path: Current
flows in the path(s) that resu/t in the /owest expenditure
of energy. At low frequency, this is accomplished
by minimizing PR losses. At high frequency,
current flows in the path(s) that minimize
inductive energy -energy transfer to and from the
magnetic field generated by the current flow." In other words, "path of least resistance" at low frequencies, "path of least impedance" at high frequencies. |
|
|
|
Post by reTrEaD on Jan 10, 2018 0:59:58 GMT -5
this is accomplished by minimizing PR losses. That's funny! The characters from that PDF don't copy/paste well. When I first read that, I just assumed it was another one of those EM science things about which I'm clueless. So I went back to the PDF to see if I could get even a clue as to what PR losses are, from context. Turns out, it's I 2R losses. Oh, okay. I feel slightly less ignorant now. |
|
|
|
Post by pablogilberto on Feb 5, 2021 21:47:43 GMT -5
Hi antigua! I just want to ask if have you found out the answer to this? I mean, how do we really minimize the coil capacitance when it comes to winding pattern and tension? Is there a clear guideline on how to properly do it? Have you also experimented with single vs heavy build wire and compare the resulting capacitances? Thank you! |
|
|
|
Post by antigua on Feb 6, 2021 13:35:12 GMT -5
Hi antigua! I just want to ask if have you found out the answer to this? I mean, how do we really minimize the coil capacitance when it comes to winding pattern and tension? Is there a clear guideline on how to properly do it? Have you also experimented with single vs heavy build wire and compare the resulting capacitances? Thank you! I haven't done any further testing with this, mostly because it among the tedious sort of testing. I have to set up for legitimate pickup production to do it. I have a new thought about this that I overlooked, because all of these reference materials are about inductors, where inductance is wanted, but with guitar pickup, neither the inductance nor the capacitance is actually wanted. This is more like a transformer, where inductance represents an inefficiency, so in the case of a guitar pickup, all this really serves to do is change the geometry of the coil, and the goal is to make it link more efficiently with the guitar strings, and less efficiently with itself. In a sense, a PAF style humbucker is an ideal example of that concept, it splits the coil into two halves, and puts each half close to the guitar strings, and as a result, L and C both drop, while voltage output goes way up. So for practical purposes, talking about insulation thickness and the like is a waste of time compared to overall coil geometry, and the magnetic circuit. There was thread on here talking about how to model the guitar string as a magnet, and that would have something to say about where the coil is most efficiently placed with respect to the pole piece and string. When the core (pole piece) is of high permeability, it's best to have the coil wrapped close to the permeable pole piece, since the pole piece is reactive to the guitar string. If the pole pieces were a non permeable type, such as a ceramic bar, then a wider coil, like a P-90 might make more sense, since the coil would have to be placed in a way that is ideal with respect to the magnetic field of the guitar strings, not the pole pieces of the pickup. But then again, in that setup, the output voltage ends up being lower no matter what, since the pole piece no longer serves to magnify the magnetic field of the guitar strings, so it's not really even worth considering, for production pickups. As as aside though, I'm curious if the fold back technique would reduce capacitance without also reducing the inductance, according to this allanfaulds.weebly.com/uploads/2/1/2/7/21271896/transformer-and-inductor-design-handbook_chapter_17.pdf it should, but you would need a CNC pickup winder to create such a coil, and I only have a Mojotone hand guided winder. It looks like it might only reduce the capacitance by a small percentage, so regardless of whether it's a good idea, it wouldn't be economical, unless you were using a CNC winder already. |
|
|
|
Post by aquin43 on Feb 10, 2021 10:57:49 GMT -5
I tried a little calculation to see if there would be a major difference in effective capacitance between the two different winding methods. I assumed that the physical capacitances, turn to next layer adjacent turn, would be equal to one another and the same in both configurations. The effective capacitance would then depend on the voltage difference across each physical capacitance. For the sake of simplicity I assume identical layers with 1V induced from end to end of a layer and consider only the capacitance between immediately adjacent wires in two layers. This needs a diagram and a sigma sign so to save effort I scribbled it down and photographed it. 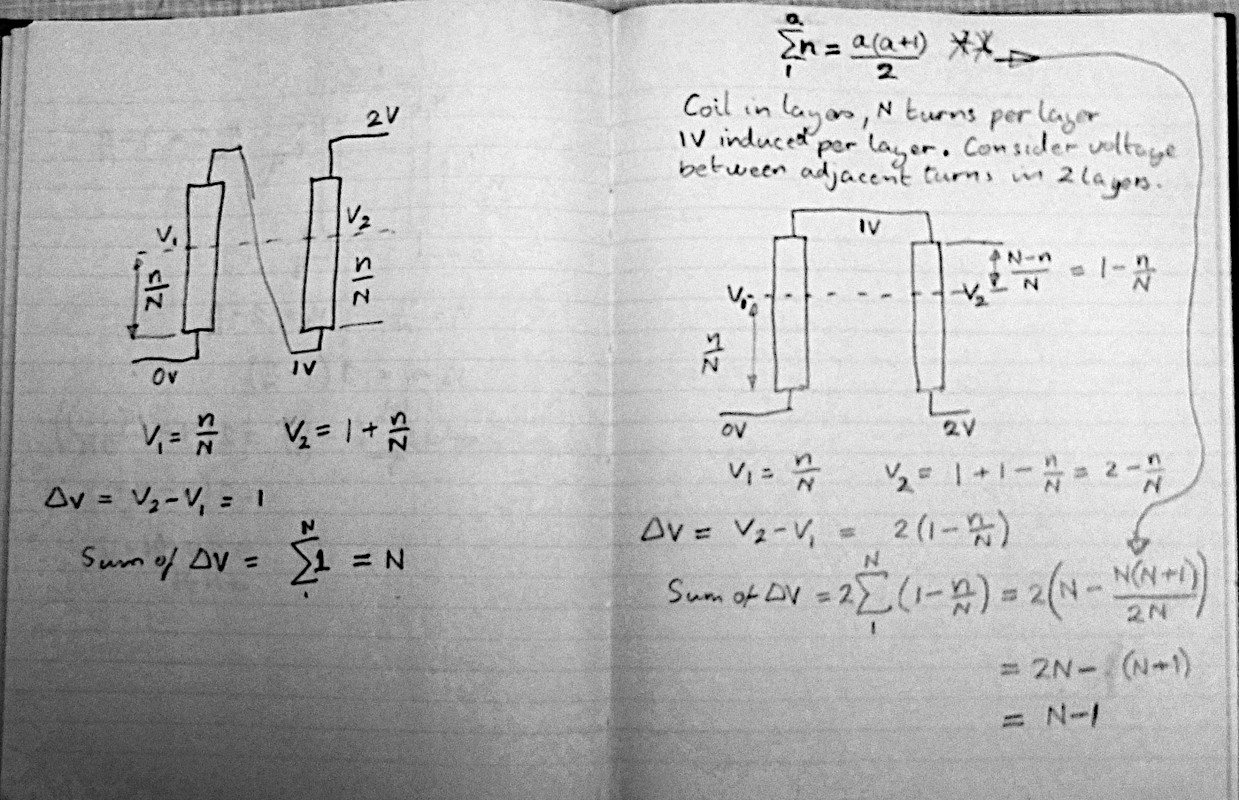 Given the assumptions made, I see no practical difference with a reasonable number of turns per layer.
|
|
|
|
Post by ziggystardust723 on Feb 14, 2021 5:20:19 GMT -5
Hello,
I did't read all the Threads, cause too difficult for me:
- a french guy 66yo who been leearned 'Entlish' at School 40y ago, & don't have to speak other than french..
But I wind Pickups since 8y on a little Schatten, Hand-Guided style.
I did't understand so much the real Question in 1st:
> but the last Sentence maybe resume all what had been said for me,
> & the difference we can see trully:
= is than on the Market of Pickups selling, there's no place to take time to:
- Handmade a pickup: like Many Brands Say.. the 0nly real Handmade pickups were the 1st 'Lipsticks' that's all,
- & so: Hand-Guided windings, cause it takes too Much Time to do,
(but the Very Best Thru Sound.!)
> So, the last mode is to wind pickups 'Scatterwound':
= on CNC999, like the only one 'Tonerider' says,
> but than Every Brands Use, & say than their pickups are Handmade..
- The Scatterwound Machine like CNC999 Try to Reproduce the Hand-Guided style,
> by be able to Change the distance to the Next lay of winding,
= But 0nly 1Time gor All the winding
> It's really Far-Away of Hand-Guided Winding: wich stills the Best kind of Winding I know to day,
- cause it's the only 1 which gives the Real Best Sound for a Pickup,
> but not the easyest, shure..
- & No Potting.. I bought 1: 8y ago,
& is still new in his pack..
- Potting is only for pickups made Facyory (1st Paf were not because the bobbins were made at the beginnibg with Butyrate: & got much better Sound.. I saw 1 on E-Bay 2y ago: 3.000€ for a '58, not for a Set.. 0n 'Leesona 102' Machines.. not Hand-Guided Machines like at 7ender: but from 1948 to End of '64: before CBS bought 7ender & made All the Pickups 'Factory': on Automatic Machines..)
- I'm a french guy, no speaking well, but I know a lot about History of Pickups since 1932 with the 1st Horse-Shoe (Awg38 & Heavy-Formvar),
& Know what make the Sound in pickups
- So I don't understand a lot these kinds of questions, cause I don't see what can happend on Sound really..
Bye, Ziggy (France, 11h20)
|
|
|
|
Post by antigua on Feb 14, 2021 17:33:23 GMT -5
I tried a little calculation to see if there would be a major difference in effective capacitance between the two different winding methods. I assumed that the physical capacitances, turn to next layer adjacent turn, would be equal to one another and the same in both configurations. The effective capacitance would then depend on the voltage difference across each physical capacitance. For the sake of simplicity I assume identical layers with 1V induced from end to end of a layer and consider only the capacitance between immediately adjacent wires in two layers. This needs a diagram and a sigma sign so to save effort I scribbled it down and photographed it.  Given the assumptions made, I see no practical difference with a reasonable number of turns per layer.
Thanks for working that out. If there was an error in your math, I wouldn't know it, but your conclusion fits with my general observation that the coil shape is more determinative than the individual layers. For example, a Jazzmaster pickup has the same amount of wire as a Strat pickup, but has a very flat coil, and around 45pF capacitance, where as a taller Strat coil is usually closer to 100pF. I think the reducing the turn to turn capacitance is more meaningful when the coil is very tall and thin, even more so than a Strat pickup. |
|
|
|
Post by Yogi B on Feb 16, 2021 4:07:23 GMT -5
Warning/Apologies: there's plenty of math(s) ahead so you'll need to be using the desktop site if you want to view it rendered out. If there was an error in your math, I wouldn't know it Well I think there is, but I also don't think I understand what aquin43 is trying to show. I believe the summations should be over the range 0 to N, not 1 to N. For the left-hand diagram, this makes: \text{sum of } \Delta V = \sum_0^N 1 = 1 + \sum_1^N 1 = N + 1And for the right-hand diagram, you'd have: \begin{aligned}
\text{sum of } \Delta V &= 2 \sum_0^N \left( 1 - {n \over N} \right)
\\[1.3em] &= 2 \left( 1 - {0 \over N} \right) + 2 \sum_1^N \left( 1 - {n \over N} \right)
\\[1.3em] &= 2(1) + (N - 1)
\\[1em] &= N + 1
\end{aligned}In other words: the sum of the voltage differences between two layers of windings (each layer with V Volts across it) at N+1 points (presumably from separating each layer into its N individual turns) is N+1 (multiplied by V, which in this case was 1V) -- and this is the same whether the winding pattern is the "U" type or "Foldback" type*. I don't disagree with that, but since that is not being directly related to capacitance, I don't know that it would tell us anything useful even if there was a difference between the results. *Personally I find these terms confusing, intuitively "Foldback" would mean the same as what is meant by "U". If we're going to use letters to represent shapes why not "U" & "N" (alternatively rotated 90°, "C" and "Z")? But I think my preferred nomenclature would be to use that of waveforms: triangle wave for "U" and sawtooth wave for "Foldback".
Since this has got my attention, here's how I'd go about it... I'll begin with pretty much the same scenario as aquin43, by 'unwinding' the turns of two adjacent winding layers into two parallel wires placed between the points A & B, but intentionally let the voltages at the extremes remain as variables:
(A: x=0) (B: x=l)
<-------- l = length -------->
Layer 2: V2a ============================== V2b
Layer 1: V1a ============================== V1b
<-- x = position -->
Potential
Difference: Va=V2a-V1a Vb=V2b-V1b
What we need now is some quantity that relates exclusively to the voltage and capacitance which can be meaningfully summed across the length the windings, such that we can calculate an equivalent lumped capacitance. The most obvious quantity that fits this description is energy, since the total electrical potential energy stored between two layers of windings must be equal to the sum of the energy stored between each subsection (assuming losses are negligible). As a reminder, the electrical potential energy, E, stored within some capacitance, C, is given by: E = {1 \over 2} C V^2
Where V is the voltage difference across the capacitance. Assuming that the voltage of each layer varies linearly across the entire length (e.g. the resistivity of the wire is constant), then so too must the voltage difference between layers vary in a linear manner, i.e. if \begin{aligned}
\operatorname{V}_1(x) &= V_{1a} + {x \over l} (V_{1b} - V_{1a})
\\[1ex] \text{and} \\[1ex]
\operatorname{V}_2(x) &= V_{2a} + {x \over l} (V_{2b} - V_{2a})
\\[1ex] \text{then} \\[1ex]
\operatorname{V}(x) &= V_a + {x \over l} (V_b - V_a)
\end{aligned}
Now, rather than separating the total length of each winding layer into N discrete subdivisions, and thus needing to worry about the start and end limits or alignment of indices, consider instead an infinitesimal section, dx, for which the stored electrical potential energy, dE, is thus given by: \begin{aligned}
\mathrm{d}E &= {1 \over 2} \cdot {C \over l} \cdot \operatorname{V}(x)^2 \cdot \mathrm{d}x
\\[1em]
&= {C \over 2 l} \left( V_a + {x \over l} (V_{b} - V_{a}) \right)^2 \mathrm{d}x
\end{aligned}
Where C/ l is the capacitance between the two windings per unit length (when considered as parallel wires), and shall be assumed to be constant along the entire length. Integrating to give the total stored energy: \begin{aligned}
E_\text{Total} = \int_0^{E_\text{Total}} \mathrm{d}E
&= {C \over 2l} \int_0^l \left( V_a + {x \over l} (V_{b} - V_{a}) \right)^2 \mathrm{d}x
\\[1em] &= {C \over 2 l} \cdot \left. {
\left( V_a + {x \over l} (V_b - V_a) \right)^3
\over
3 \cdot {\mathrm{d} \over \mathrm{d}x}\!\left( V_a + {x \over l} (V_b - V_a) \right)
} \right\rvert_{0}^{x=l}
\\[1.5em] &= {C \over 2 l} \cdot \left. {
\left( V_a + {x \over l} (V_b - V_a) \right)^3
\over
3 \left( 0 + {(V_b - V_a) \over l} \right)
} \right\rvert_{0}^{x=l}
\\[1.5em] &= {C \over 2 \bcancel{l}} \cdot {\bcancel{l} \over 3 (V_b - V_a)}
\cdot \left. \left( V_a + {x \over l} (V_b - V_a) \right)^3 \right\rvert_{0}^{x=l}
\\[1.5em] &= {C \over 6 (V_b - V_a)} \cdot \left[
\left( V_a + {l \over l} (V_b - V_a) \right)^3
- \left( V_a + {0 \over l} (V_b - V_a) \right)^3
\right]
\\[1.5em] &= {C \over 6 (V_b - V_a)} \cdot \left[
\left( V_a + V_b - V_a \right)^3
- ( V_a )^3
\right]
\\[1.5em] &= {C \over 6 (V_b - V_a)} \cdot \left[
{V_b} ^3 - {V_a}^3
\right]
\\[1.5em] &= {C \over 6} \cdot { {V_b} ^3 - {V_a}^3 \over V_b - V_a }
\\[1.5em] &= {C \over 6} \cdot { \cancel{(V_b - V_a)} ({V_b}^2 + V_a V_b + {V_a}^2) \over \cancel{V_{b} - V_{a}} }
\\[1.5em] &= {C \over 6} \cdot ({V_b}^2 + V_a V_b + {V_a}^2)
\end{aligned}
Going back to our winding patterns, with a total voltage difference, V, across the two layers, for the "U" pattern we have: \begin{aligned}
V_{1a} &= 0, & V_{2a} &= V & \implies && V_a &= V - 0 = V
\\
V_{1b} &= {V \over 2},& V_{2b} &= {V \over 2} & \implies && V_b &= {V \over 2} - {V \over 2} = 0
\end{aligned}
\\[1em]\text{thus}\\[1em]
\begin{aligned}
E_\text{``U''} &= {C \over 6} \cdot (0^2 + 0V + V^2)
\\[1em]
&= {C V^2 \over 6}
\end{aligned}
Noting that this must also be equal to the total energy if calculated from the lumped capacitance, C "U": \begin{aligned}
E_\text{``U''} = {1 \over 2} C_\text{``U''} V^2 &= {C V^2 \over 6}
\\[1em] C_\text{``U''} &= {C \over 3}
\end{aligned}
Whereas for the "Foldback" winding pattern, in which we effectively exchange V 2a & V 2b, we have: \begin{aligned}
V_{1a} &= 0, & V_{2a} &= {V \over 2} & \implies && V_a &= {V \over 2} - 0 = {V \over 2}
\\[1em]
V_{1b} &= {V \over 2},& V_{2b} &= V & \implies && V_b &= V - {V \over 2} = {V \over 2}
\end{aligned}
\\[1em] \text{thus}
\\[1em] \begin{aligned}
E_\text{``Foldback''} &= {C \over 6} \cdot \left(
\left(V \over 2\right)^2
+ \left(V \over 2\right) \left(V \over 2\right)
+ \left(V \over 2\right)^2
\right)
\\[1.5em]
E_\text{``Foldback''} &= {C \over 6} \cdot 3 \cdot \left(V \over 2\right)^2
\\[1.5em] &= {C V^2 \over 8}
\end{aligned}
Again, calculating the equivalent lumped capacitance, C "Foldback": \begin{aligned}
E_\text{``Foldback''} = {1 \over 2} C_\text{``Foldback''} V^2 &= {C V^2 \over 8}
\\[1em] C_\text{``Foldback''} &= {C \over 4}
\end{aligned}
Finally, solving the two equations for lumped capacitance simultaneously gives us: C_\text{``Foldback''} = {3 \over 4} C_\text{``U''} So, assuming all the previous is correct, theoretically windings composed of the "Foldback" style should have 25% less capacitance than windings composed of the "U" style -- which may not be a huge saving, but I'd at least call it significant.
|
|
|
|
Post by aquin43 on Feb 16, 2021 11:11:27 GMT -5
Warning/Apologies: there's plenty of math(s) ahead so you'll need to be using the desktop site if you want to view it rendered out. If there was an error in your math, I wouldn't know it Well I think there is, but I also don't think I understand what aquin43 is trying to show. I believe the summations should be over the range 0 to N, not 1 to N. My original idea was that there are N turns in each layer, numbered n = 1 to N. Each turn has a mean voltage across it of 1/N volts induced by the uniform alternating magnetic field. This means that even turn 1, which is connected to zero volts, has non zero voltage. I sum from 1 to N because there is no turn zero. The distributed capacitance between the layers is assumed to be uniform in structure so that it can be reduced to a series of equal individual capacitances between corresponding turns in the layers. The currents flowing through these capacitors will be proportional to the voltages across them. The capacitor currents are tacitly assumed to be small enough not to cause a phase shift across a layer so that all voltages are in phase. It is assumed that the only way that a capacitor affects the network it is connected to by drawing a current, which leads to the assumption that the voltages across the capacitors can act as a proxy for their effective values.
-----------------------------------
One could turn this discrete model into a continuous one by unwrapping the coil as you do into two parallel strands. Without loss of generality, let the total length per layer be 1 and the distance along the length measured from the start of the first layer be x. We would then integrate x from 0 to 1.
The integrated voltage across the uniformly distributed capacitance would act as a proxy for the capacitive current drawn, making it a relative measure of the effective capacitance. We would then have
Normal case: V1 = x, V2 = 2-x, delta V = 2(1 - x)
1 1
integral 2(1-x) = 2[ x - x^2/2 ] = 1
0 0
Foldback case: V1 = x, V2 = 1+x, delta V = 1
1 1
integral 1 = [ x ] = 1
0 0The capacitive current is the same in both cases.
Edit: 17 Feb
Although the average voltage differences between layers are the same, the two distributions of these voltages are very different so that the assumption that the capacitive currents don't affect the voltages along the wire becomes crucial. This assumption may not be valid and more detailed modelling may be required.
|
|
|
|
Post by Yogi B on Feb 17, 2021 21:53:38 GMT -5
My original idea was that there are N turns in each layer, numbered n = 1 to N. Each turn has a mean voltage across it of 1/N volts induced by the uniform alternating magnetic field. This means that even turn 1, which is connected to zero volts, has non zero voltage. I sum from 1 to N because there is no turn zero. What's so special about the first turn? The last turn is connected to 2V, yet (in your calculations for the "Foldback" style) you count its voltage as 2V, not some value strictly less than 2V. Additionally, what's so special about the first turn of the first layer? For the "U" style winding the first turn of the second layer is where you have n = N, and your calculated voltage is 1 + (1 - N/N) = 1V, i.e. voltage equal to that of the last turn of the first layer -- not some value strictly greater than 1V.
It took me longer than it should've, but I did manage to figure out by myself that you were calculating the (arithmetic) mean of ΔV. I didn't realise it sooner because you're doing the division step first (to the summand/integrand) rather than after (to the sum/integral), as I might normally expect, but the result is the same. However I still don't know how that's supposed to tell us anything useful about the capacitance. Why? Because V = IZ? Given V = IZ, current is only proportional to voltage if the impedance is constant. If the effective capacitance were to vary along the length of the windings then this is no longer true. In other words, by assuming that the current and voltage are proportional you are also assuming that the effective capacitance is constant. Furthermore:Why would that give a proxy for just the capacitive current? The voltage difference along the length of each turn/layer must also cause current draw along the windings -- the total current is not just that which is due to the capacitance. |
|
|
|
Post by aquin43 on Feb 18, 2021 5:23:20 GMT -5
My original idea was that there are N turns in each layer, numbered n = 1 to N. Each turn has a mean voltage across it of 1/N volts induced by the uniform alternating magnetic field. This means that even turn 1, which is connected to zero volts, has non zero voltage. I sum from 1 to N because there is no turn zero. What's so special about the first turn? The last turn is connected to 2V, yet (in your calculations for the "Foldback" style) you count its voltage as 2V, not some value strictly less than 2V. Additionally, what's so special about the first turn of the first layer? For the "U" style winding the first turn of the second layer is where you have n = N, and your calculated voltage is 1 + (1 - N/N) = 1V, i.e. voltage equal to that of the last turn of the first layer -- not some value strictly greater than 1V.
It took me longer than it should've, but I did manage to figure out by myself that you were calculating the (arithmetic) mean of ΔV. I didn't realise it sooner because you're doing the division step first (to the summand/integrand) rather than after (to the sum/integral), as I might normally expect, but the result is the same. However I still don't know how that's supposed to tell us anything useful about the capacitance. Why? Because V = IZ? Given V = IZ, current is only proportional to voltage if the impedance is constant. If the effective capacitance were to vary along the length of the windings then this is no longer true. In other words, by assuming that the current and voltage are proportional you are also assuming that the effective capacitance is constant. Furthermore:Why would that give a proxy for just the capacitive current? The voltage difference along the length of each turn/layer must also cause current draw along the windings -- the total current is not just that which is due to the capacitance. In my last post I effectively abandoned my initial turns based argument with its accounting problems in favour of your suggestion of unwinding the layers and considering them as parallel wires.
The two winding methods then give voltage differences between corresponding points of 1V or 2(1-x)V, both of which integrate to 1V over the length of the wires. This is based on the simplifying assumption that the wires are immersed in a uniform alternating magnetic field which induces a constant voltage per length of the wire.
Obviously, the physical capacitance between the two wires is the same in both wiring configurations. If there is to be a difference in the measured capacitance, it can only be caused by the different voltage distributions. Nothing else changes.
My simple argument is that the effect of a capacitor on a circuit is directly dependent on the voltage that the circuit would place across the points where the capacitor is to be attached. A capacitor with zero volts across it does nothing.
What we are computing, therefore, is the distribution of voltages in the absence of any capacitance and their sum. We further make the assumption that the loading of the capacitance on the network can be small enough to be considered zero. This seems plausible, given that the wire is copper, the inductance per layer is very small and we can assume an arbitrary working frequency.
Under these conditions, the voltages will act as a proxies for the currents drawn by the capacitances and will provide a relative measure of the effective capacitance as seen by the network.
A further step might be to simulate a discrete version of this arrangement with Spice.
|
|
|
|
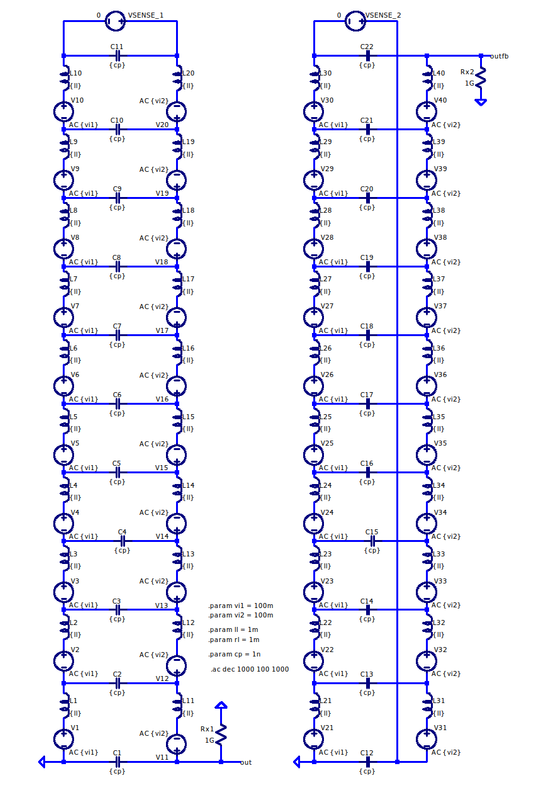
Post by aquin43 on Feb 18, 2021 11:29:27 GMT -5
I tried an LTSpice simulation of a pair of 10 turn layers The total currents through the capacitors are I(VSENSE_1) and I(VSENSE_2). They prove to be equal. The output voltages out and outfb differ slightly at higher frequencies and outfb seems to be the most affected.
C11 is shorted out by VSENSE_1 but is included anyway. The inductors all have resistance, the voltage sources represent the volts per turn and everything is parameterised. The values are arbitrary but chosen so that the capacitive loading on each node is negligible.
The simulation file, to be copied into a text editor by anyone interested and saved as pu-turns.asc is: Version 4
SHEET 1 2176 1492
WIRE 176 -1232 48 -1232
WIRE 416 -1232 256 -1232
WIRE 960 -1232 864 -1232
WIRE 1136 -1232 1040 -1232
WIRE 48 -1120 48 -1232
WIRE 192 -1120 48 -1120
WIRE 416 -1120 416 -1232
WIRE 416 -1120 256 -1120
WIRE 864 -1120 864 -1232
WIRE 1008 -1120 864 -1120
WIRE 1232 -1120 1072 -1120
WIRE 1408 -1120 1232 -1120
WIRE 1440 -1120 1408 -1120
WIRE 48 -1088 48 -1120
WIRE 416 -1088 416 -1120
WIRE 864 -1088 864 -1120
WIRE 1232 -1088 1232 -1120
WIRE 1408 -1088 1408 -1120
WIRE 48 -976 48 -1008
WIRE 416 -976 416 -1008
WIRE 864 -976 864 -1008
WIRE 1232 -976 1232 -1008
WIRE 1408 -976 1408 -1008
WIRE 48 -880 48 -896
WIRE 192 -880 48 -880
WIRE 416 -880 416 -896
WIRE 416 -880 256 -880
WIRE 864 -880 864 -896
WIRE 1008 -880 864 -880
WIRE 1232 -880 1232 -896
WIRE 1232 -880 1072 -880
WIRE 48 -864 48 -880
WIRE 416 -864 416 -880
WIRE 864 -864 864 -880
WIRE 1232 -864 1232 -880
WIRE 48 -752 48 -784
WIRE 416 -752 416 -784
WIRE 864 -752 864 -784
WIRE 1232 -752 1232 -784
WIRE 48 -656 48 -672
WIRE 192 -656 48 -656
WIRE 416 -656 416 -672
WIRE 416 -656 256 -656
WIRE 864 -656 864 -672
WIRE 1008 -656 864 -656
WIRE 1232 -656 1232 -672
WIRE 1232 -656 1072 -656
WIRE 48 -640 48 -656
WIRE 416 -640 416 -656
WIRE 864 -640 864 -656
WIRE 1232 -640 1232 -656
WIRE 48 -528 48 -560
WIRE 416 -528 416 -560
WIRE 864 -528 864 -560
WIRE 1232 -528 1232 -560
WIRE 48 -432 48 -448
WIRE 192 -432 48 -432
WIRE 416 -432 416 -448
WIRE 416 -432 256 -432
WIRE 864 -432 864 -448
WIRE 1008 -432 864 -432
WIRE 1232 -432 1232 -448
WIRE 1232 -432 1072 -432
WIRE 48 -416 48 -432
WIRE 416 -416 416 -432
WIRE 864 -416 864 -432
WIRE 1232 -416 1232 -432
WIRE 48 -304 48 -336
WIRE 416 -304 416 -336
WIRE 864 -304 864 -336
WIRE 1232 -304 1232 -336
WIRE 48 -208 48 -224
WIRE 192 -208 48 -208
WIRE 416 -208 416 -224
WIRE 416 -208 256 -208
WIRE 864 -208 864 -224
WIRE 1008 -208 864 -208
WIRE 1232 -208 1232 -224
WIRE 1232 -208 1072 -208
WIRE 48 -192 48 -208
WIRE 416 -192 416 -208
WIRE 864 -192 864 -208
WIRE 1232 -192 1232 -208
WIRE 48 -80 48 -112
WIRE 416 -80 416 -112
WIRE 864 -80 864 -112
WIRE 1232 -80 1232 -112
WIRE 48 16 48 0
WIRE 192 16 48 16
WIRE 416 16 416 0
WIRE 416 16 256 16
WIRE 864 16 864 0
WIRE 1008 16 864 16
WIRE 1232 16 1232 0
WIRE 1232 16 1072 16
WIRE 48 32 48 16
WIRE 416 32 416 16
WIRE 864 32 864 16
WIRE 1232 32 1232 16
WIRE 48 144 48 112
WIRE 416 144 416 112
WIRE 864 144 864 112
WIRE 1232 144 1232 112
WIRE 48 240 48 224
WIRE 192 240 48 240
WIRE 416 240 416 224
WIRE 416 240 256 240
WIRE 864 240 864 224
WIRE 1008 240 864 240
WIRE 1232 240 1232 224
WIRE 1232 240 1072 240
WIRE 48 256 48 240
WIRE 416 256 416 240
WIRE 864 256 864 240
WIRE 1232 256 1232 240
WIRE 48 368 48 336
WIRE 416 368 416 336
WIRE 864 368 864 336
WIRE 1232 368 1232 336
WIRE 48 464 48 448
WIRE 208 464 48 464
WIRE 416 464 416 448
WIRE 416 464 272 464
WIRE 864 464 864 448
WIRE 1024 464 864 464
WIRE 1232 464 1232 448
WIRE 1232 464 1088 464
WIRE 48 480 48 464
WIRE 416 480 416 464
WIRE 864 480 864 464
WIRE 1232 480 1232 464
WIRE 48 592 48 560
WIRE 416 592 416 560
WIRE 864 592 864 560
WIRE 1232 592 1232 560
WIRE 48 688 48 672
WIRE 192 688 48 688
WIRE 416 688 416 672
WIRE 416 688 256 688
WIRE 864 688 864 672
WIRE 1008 688 864 688
WIRE 1232 688 1232 672
WIRE 1232 688 1072 688
WIRE 48 704 48 688
WIRE 416 704 416 688
WIRE 864 704 864 688
WIRE 1232 704 1232 688
WIRE 48 816 48 784
WIRE 864 816 864 784
WIRE 1232 816 1232 784
WIRE 416 832 416 784
WIRE 48 928 48 896
WIRE 192 928 48 928
WIRE 416 928 416 912
WIRE 416 928 256 928
WIRE 864 928 864 896
WIRE 1008 928 864 928
WIRE 1232 928 1232 896
WIRE 1232 928 1072 928
WIRE 48 960 48 928
WIRE 416 960 416 928
WIRE 864 960 864 928
WIRE 1232 960 1232 928
WIRE 560 1056 560 1008
WIRE 48 1072 48 1040
WIRE 864 1072 864 1040
WIRE 1232 1072 1232 1040
WIRE 416 1088 416 1040
WIRE 48 1184 48 1152
WIRE 48 1184 -16 1184
WIRE 192 1184 48 1184
WIRE 416 1184 416 1168
WIRE 416 1184 256 1184
WIRE 560 1184 560 1136
WIRE 560 1184 416 1184
WIRE 624 1184 560 1184
WIRE 864 1184 864 1152
WIRE 864 1184 816 1184
WIRE 1008 1184 864 1184
WIRE 1136 1184 1136 -1232
WIRE 1136 1184 1072 1184
WIRE 1232 1184 1232 1152
WIRE 1232 1184 1136 1184
FLAG -16 1184 0
FLAG 560 1008 0
FLAG 816 1184 0
FLAG 1408 -976 0
FLAG 624 1184 out
FLAG 1440 -1120 outfb
SYMBOL ind 32 944 R0
SYMATTR InstName L1
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 1056 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V1
SYMATTR Value ""
SYMBOL ind 32 688 R0
SYMATTR InstName L2
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 800 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V2
SYMATTR Value ""
SYMBOL ind 32 464 R0
SYMATTR InstName L3
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 576 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V3
SYMATTR Value ""
SYMBOL ind 32 240 R0
SYMATTR InstName L4
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 352 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V4
SYMATTR Value ""
SYMBOL ind 32 16 R0
SYMATTR InstName L5
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 128 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V5
SYMATTR Value ""
SYMBOL ind 32 -208 R0
SYMATTR InstName L6
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 -96 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V6
SYMATTR Value ""
SYMBOL ind 32 -432 R0
SYMATTR InstName L7
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 -320 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V7
SYMATTR Value ""
SYMBOL ind 32 -656 R0
SYMATTR InstName L8
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 -544 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V8
SYMATTR Value ""
SYMBOL ind 32 -880 R0
SYMATTR InstName L9
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 -768 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V9
SYMATTR Value ""
SYMBOL ind 32 -1104 R0
SYMATTR InstName L10
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 48 -992 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V10
SYMATTR Value ""
SYMBOL ind 400 944 R0
SYMATTR InstName L11
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 1184 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V11
SYMATTR Value ""
SYMBOL ind 400 688 R0
SYMATTR InstName L12
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 928 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V12
SYMATTR Value ""
SYMBOL ind 400 464 R0
SYMATTR InstName L13
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 688 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V13
SYMATTR Value ""
SYMBOL ind 400 240 R0
SYMATTR InstName L14
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 464 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V14
SYMATTR Value ""
SYMBOL ind 400 16 R0
SYMATTR InstName L15
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 240 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V15
SYMATTR Value ""
SYMBOL ind 400 -208 R0
SYMATTR InstName L16
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 16 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V16
SYMATTR Value ""
SYMBOL ind 400 -432 R0
SYMATTR InstName L17
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 -208 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V17
SYMATTR Value ""
SYMBOL ind 400 -656 R0
SYMATTR InstName L18
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 -432 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V18
SYMATTR Value ""
SYMBOL ind 400 -880 R0
SYMATTR InstName L19
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 -656 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V19
SYMATTR Value ""
SYMBOL ind 400 -1104 R0
SYMATTR InstName L20
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 416 -880 R180
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V20
SYMATTR Value ""
SYMBOL res 576 1152 R180
WINDOW 0 36 76 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName Rx1
SYMATTR Value 1G
SYMBOL cap 256 1168 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C1
SYMATTR Value {cp}
SYMBOL cap 256 912 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C2
SYMATTR Value {cp}
SYMBOL cap 256 672 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C3
SYMATTR Value {cp}
SYMBOL cap 272 448 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C4
SYMATTR Value {cp}
SYMBOL cap 256 224 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C5
SYMATTR Value {cp}
SYMBOL cap 256 0 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C6
SYMATTR Value {cp}
SYMBOL cap 256 -224 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C7
SYMATTR Value {cp}
SYMBOL cap 256 -448 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C8
SYMATTR Value {cp}
SYMBOL cap 256 -672 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C9
SYMATTR Value {cp}
SYMBOL cap 256 -896 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C10
SYMATTR Value {cp}
SYMBOL cap 256 -1136 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C11
SYMATTR Value {cp}
SYMBOL ind 848 944 R0
SYMATTR InstName L21
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 1056 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V21
SYMATTR Value ""
SYMBOL ind 848 688 R0
SYMATTR InstName L22
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 800 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V22
SYMATTR Value ""
SYMBOL ind 848 464 R0
SYMATTR InstName L23
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 576 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V23
SYMATTR Value ""
SYMBOL ind 848 240 R0
SYMATTR InstName L24
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 352 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V24
SYMATTR Value ""
SYMBOL ind 848 16 R0
SYMATTR InstName L25
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 128 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V25
SYMATTR Value ""
SYMBOL ind 848 -208 R0
SYMATTR InstName L26
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 -96 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V26
SYMATTR Value ""
SYMBOL ind 848 -432 R0
SYMATTR InstName L27
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 -320 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V27
SYMATTR Value ""
SYMBOL ind 848 -656 R0
SYMATTR InstName L28
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 -544 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V28
SYMATTR Value ""
SYMBOL ind 848 -880 R0
SYMATTR InstName L29
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 -768 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V29
SYMATTR Value ""
SYMBOL ind 848 -1104 R0
SYMATTR InstName L30
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 864 -992 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi1}
SYMATTR InstName V30
SYMATTR Value ""
SYMBOL ind 1216 944 R0
SYMATTR InstName L31
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 1056 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V31
SYMATTR Value ""
SYMBOL ind 1216 688 R0
SYMATTR InstName L32
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 800 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V32
SYMATTR Value ""
SYMBOL ind 1216 464 R0
SYMATTR InstName L33
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 576 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V33
SYMATTR Value ""
SYMBOL ind 1216 240 R0
SYMATTR InstName L34
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 352 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V34
SYMATTR Value ""
SYMBOL ind 1216 16 R0
SYMATTR InstName L35
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 128 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V35
SYMATTR Value ""
SYMBOL ind 1216 -208 R0
SYMATTR InstName L36
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 -96 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V36
SYMATTR Value ""
SYMBOL ind 1216 -432 R0
SYMATTR InstName L37
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 -320 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V37
SYMATTR Value ""
SYMBOL ind 1216 -656 R0
SYMATTR InstName L38
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 -544 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V38
SYMATTR Value ""
SYMBOL ind 1216 -880 R0
SYMATTR InstName L39
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 -768 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V39
SYMATTR Value ""
SYMBOL ind 1216 -1104 R0
SYMATTR InstName L40
SYMATTR Value {ll}
SYMATTR SpiceLine Rser={rl}
SYMBOL voltage 1232 -992 R0
WINDOW 123 17 95 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value2 AC {vi2}
SYMATTR InstName V40
SYMATTR Value ""
SYMBOL res 1424 -992 R180
WINDOW 0 36 76 Left 2
WINDOW 3 36 40 Left 2
SYMATTR InstName Rx2
SYMATTR Value 1G
SYMBOL cap 1072 1168 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C12
SYMATTR Value {cp}
SYMBOL cap 1072 912 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C13
SYMATTR Value {cp}
SYMBOL cap 1072 672 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C14
SYMATTR Value {cp}
SYMBOL cap 1088 448 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C15
SYMATTR Value {cp}
SYMBOL cap 1072 224 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C16
SYMATTR Value {cp}
SYMBOL cap 1072 0 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C17
SYMATTR Value {cp}
SYMBOL cap 1072 -224 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C18
SYMATTR Value {cp}
SYMBOL cap 1072 -448 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C19
SYMATTR Value {cp}
SYMBOL cap 1072 -672 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C20
SYMATTR Value {cp}
SYMBOL cap 1072 -896 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C21
SYMATTR Value {cp}
SYMBOL cap 1072 -1136 R90
WINDOW 0 0 32 VBottom 2
WINDOW 3 32 32 VTop 2
SYMATTR InstName C22
SYMATTR Value {cp}
SYMBOL voltage 272 -1232 R90
WINDOW 39 0 0 Left 0
WINDOW 0 -21 -106 VRight 2
WINDOW 3 -22 102 VRight 2
SYMATTR InstName VSENSE_1
SYMATTR Value 0
SYMBOL voltage 1056 -1232 R90
WINDOW 39 0 0 Left 0
WINDOW 0 -22 -97 VRight 2
WINDOW 3 -22 102 VRight 2
SYMATTR InstName VSENSE_2
SYMATTR Value 0
TEXT 528 880 Left 2 !.ac dec 1000 100 1000
TEXT 520 752 Left 2 !.param ll = 1m
TEXT 520 784 Left 2 !.param rl = 1m
TEXT 520 704 Left 2 !.param vi2 = 100m
TEXT 520 672 Left 2 !.param vi1 = 100m
TEXT 520 832 Left 2 !.param cp = 1n
The next exercise would be to model the two voltage distributions in FEMM to check whether the stored charges would be equal. |
|
|
|
Post by Yogi B on Feb 19, 2021 0:51:18 GMT -5
I tried an LTSpice simulation of a pair of 10 turn layers ... The total currents through the capacitors are I(VSENSE_1) and I(VSENSE_2). They prove to be equal. Equal-schmequal, looking at higher frequencies: The (first) resonant peak for I(VSENSE_1) is at roughly 16.827kHz, whereas for I(VSENSE_2) it is at 18.880kHz. Taking the square of the ratio of these resonant frequencies gives us an approximate ratio of the lumped LC for each winding style: (16820 / 18862)2 ≈ 0.79520 ≈ (LFB × CFB) / (LU × CU) Assuming that L U = L FB, therefore gives: CFB ≈ 0.79520 CU Which is relatively close to my result from earlier: Finally, solving the two equations for lumped capacitance simultaneously gives us: C_\text{``Foldback''} = {3 \over 4} C_\text{``U''} |
|
|
|
Post by aquin43 on Feb 19, 2021 6:47:13 GMT -5
I tried an LTSpice simulation of a pair of 10 turn layers ... The total currents through the capacitors are I(VSENSE_1) and I(VSENSE_2). They prove to be equal. Equal-schmequal, looking at higher frequencies: My description should have been more rigorous. The values I used in the simulation were arbitrary as I stated but on the tacit understanding that the result would only be meaningful well below the various resonances. These resonances are artefacts of the model which, because I included a representation of the inductance and resistance per turn, behaves ultimately as two coupled transmission lines. For more realistic values, assume a pickup with 2H, 6kOhms, 150pF, 7000 turns and a guess of 100 turns per layer giving 70 layers. . The resistance per turn will be 875m, resistance per layer 87.5, making rl 8.75. The inductance per turn will be 2/7000^2 = 41n, inductance per layer 410u making ll = 41u (the L's in the model are not coupled) Assuming that the layer capacitances add gives a capacitance per layer of 2.14pF, making cp = 214fF. With these values, the two currents are dominated by the capacitance up to the first parasitic resonance above 5MHz. They appear to be equal, with a phase angle very close to 90 degrees. I take that to mean that the currents between layers are equal and capacitive in both configurations, implying that the effective inter layer capacitances are the same.
Increasing the number of divisions to the full 100 would, presumably, raise the frequency of the resonance artefacts even further from the audio range.
Edit: Rx1 and Rx2 should be removed. They are unnecessary and cause errors in the behaviour of the model at low frequencies.
|
|
tms9
Rookie Solder Flinger

Posts: 1
Likes: 0
|
Post by tms9 on Feb 23, 2021 19:49:17 GMT -5
I don't follow exactly, but I'll tell you that new guitar based music is still highly marketable, but not only that, there's always renewed interest in heroes of the past, like Jimi Hendrix, Beatles, David Bowie, because we live in a day and age where society no longer elevates anyone to such a mythical status, and because music was one of the few staple forms of entertainment at the time, they put a lot of effort into their craft, relative to today, where most music is mostly composed of production magic, style over substance. A given piece of music doesn't generate as much money, so it has to be created for less money. existence of an ever growing back catalog just further depresses the value of new content. I think the real difference is that, in the 60-70s, there was a push to try new things, such as the Alembic guitars with a dozen switches and built in pre amps, but all of that failed to catch on, and by the 80's, everyone went nuts for high output pickups and Floyd Rose trems, but by the 90's, and ever since, people either want stock guitars, or 50's vintage guitars. There no longer much interest in experimentation, nor heavy modding, and so that keeps guitarists from taking too great an interest in the finer workings of pickups. They're interested in the dimensionless quantity of mojo, and little else. I realize I'm late to the thread, but I love this: "[T]he dimensionless quantity of mojo". I also think that this is a pretty compelling analysis of the role of the electric guitar over time, and a nice explanation of how we ended up where we seem to be right now. Though I'd add that there's a distressing element of anti-science attitude, an attitude of "you have your truth and I have mine", which came out of both philosophy of science (e.g. Kuhn) and postmodernist literary theory (e.g. Derrida), and has ironically been embraced by the left and the right, at least in the US. |
|
|
|
Post by ms on Feb 24, 2021 12:28:01 GMT -5
I do not think that it is a anti-science to recognize what sets the overall frequency response of the system and not mess with it. Add a preamp and you can have whatever frequency response you want. This includes especially more high frequencies, almost certainly not what you want. Add a preamp and you have to include a way to keep the sound the way it was before you added it as one possibility.
Limitations in the system establish an essential part of its character, which of course you can achieve by other more complicated means if you want.
|
|
|
|
Post by antigua on Feb 24, 2021 22:35:51 GMT -5
I tried an LTSpice simulation of a pair of 10 turn layers
The total currents through the capacitors are I(VSENSE_1) and I(VSENSE_2). They prove to be equal. The output voltages out and outfb differ slightly at higher frequencies and outfb seems to be the most affected.
C11 is shorted out by VSENSE_1 but is included anyway. The inductors all have resistance, the voltage sources represent the volts per turn and everything is parameterised. The values are arbitrary but chosen so that the capacitive loading on each node is negligible.
The simulation file, to be copied into a text editor by anyone interested and saved as pu-turns.asc is: ...
The next exercise would be to model the two voltage distributions in FEMM to check whether the stored charges would be equal. So this models the capacitance of two wires that are side by side, but it seems that the lumped capacitance is gradient that extends from the first wind to the very last, so the capacitance individual turns as depicted is but a small part of the lump. Maybe it's 0.1% or 10%, I have no idea. I think in the transformer designs where they use the fold back technique, there might have been a less layers, and they might have been used for RF, so the improvement would have been more meaningful. |
|