Active preamp wiring

[fleepd]

Hey, i'm new here. I have HSS guitar with Suhr pickups, and I want to try Bajaman guitar preamp in differential mode, but I don't want to make my guitar permanently active, so i'm trying to come up with a switching scheme so that I could use both passive and active modes. So far, I ended up with this: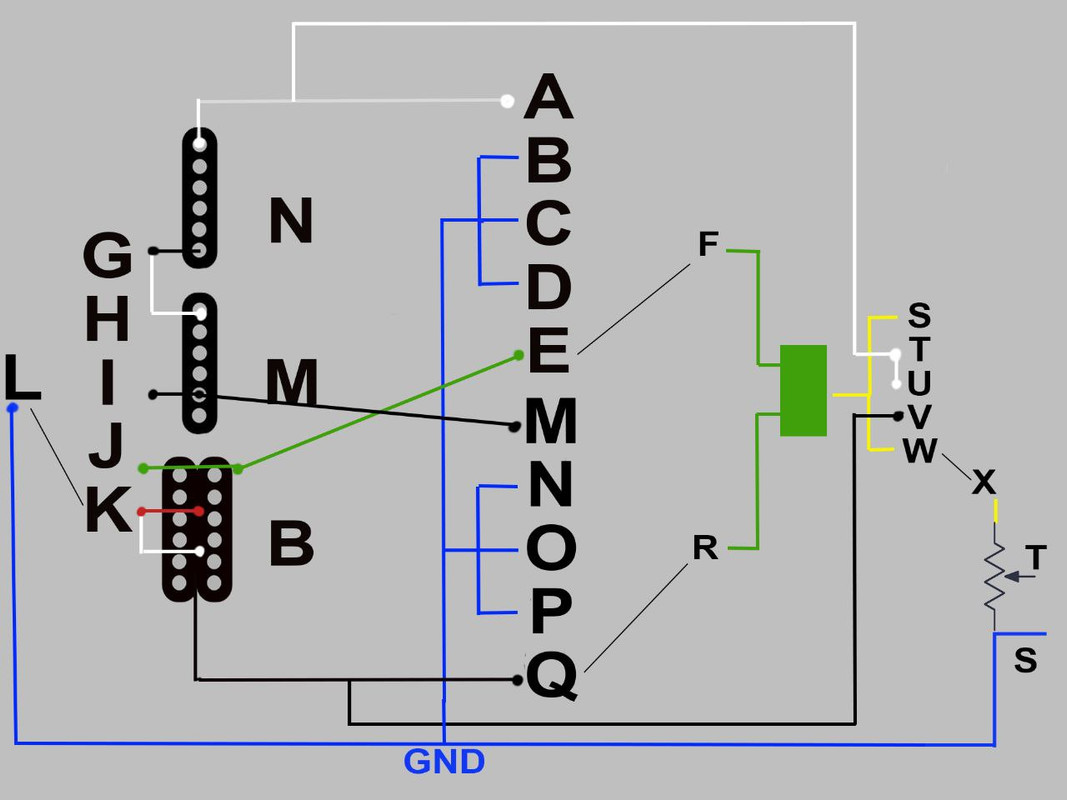




The switch is Schaller Megaswitch M, F and R lugs go to + and - inputs of differential preamp. Middle pickup is RWRP. This is what i think it should do:

1	Bridge Active (both coils in parallel, out of phase, hum in phase)
2	Bridge Humbucker (coils in series)
3	Neck and Middle in series
4	Neck
5	Neck + Middle Active (coils in parallel, out of phase, hum in phase)

So, my question are:
1) Does it look correct to you?
2) I have a spare dpdt push/pull pot, can this wiring can be modified to also include additional Neck + Middle in parallel and Middle only in passive mode?

[mikecg]

Hello fleepd,

I've had a stab at cleaning up your schematic and checking the connectivity:

SPOILER: Click to show

I suggest that you double check my drawing - it looks OK to me - but I might have missed something.

I had a quick look at your 'Baja' pre-amp link - and it looks like an interesting project, as far as I can see -
Effective hum cancellation using the common mode rejection of the differential input pre-amp relies on balancing the source and load impedances of the humbucker coils and the pre-amp inputs, respectively. This is covered in some detail in your linked post. I have not looked in detail at the possibility of adding your N+M in parallel, and M only requirement using a push-pull switch, but I have a sneaking suspicion that you will not have to wait too long for some help with this mod.

[fleepd]

Thanks mikecg, your schematic looks ok to me, dont think you’ve missed something. Can I ask a question what software did you use to create this diagram?

[mikecg]

Hello fleepd,

I use an old version of TurboCAD Deluxe 2D/3D, bought in a Maplin (UK) store in 2014 for £7.99!

You can download the 2D/3D 2023 trial version (free) or the full version (£79.99), from here: www.turbocad.co.uk/windows-range/

However, if you are looking for free CAD software you may want to try this: www.autodesk.com/products/fusion-360/personal

I hasten to add that I am not familiar with the autodesk product, so I cannot comment on its ease of use, but it does appear to be free for personal use.

[fleepd]

Hello again! So I've decided to base my wiring on Strat-o-various project and completely remade the diagram, which now includes 4pdt on-on switch to enable active preamp. Can someone recheck new diagram for any obvious mistakes and maybe provide some suggestions?

[mikecg]

Hello fleepd,

I see that you have made good progress using a CAD program, which one are you now using?
Also, that you are now using a modified version of reTrEaD 's 'strat-o-various' switching scheme.
I have done an initial check on your new scheme, and as far as I can see, the series active and passive configurations are correct, with the possible exception of active position 5 (neck boost). The parallel passive configuration also checks out, but the parallel active set does not seem to produce the connections listed in your table.
I think you will find that the parallel active set is the same as the parallel passive set with the obvious difference that the signal is buffered by the pre-amp. There may be a problem with series active position 5, and all the parallel active positions, in that the preamp inputs in these cases, have no ground reference, being connected between the inverting and non-inverting inputs. If this turns out to be a problem, the simplest solution may be to apply an additional switched ground to the inverting input of the preamp, so that it is grounded, only when parallel and active modes are selected. In practice, this will require an additional pole on your series-parallel switch, and the use of the unused lug adjacent to the inverting input connection, on the 4PDT switch. 

[fleepd]

Hello mikecg, thanks for your thorough review of the scheme.

I see that you have made good progress using a CAD program, which one are you now using?

I'm now using draw.io service. It's free and has electrical symbols library, though its not enabled by default, you have to find it in settings.

but the parallel active set does not seem to produce the connections listed in your table.

Yeah, I can see my mistake now. Somehow I thought that SL junction will be grounded in active parallel position, but it's not the case in the schematic.

There may be a problem with series active position 5, and all the parallel active positions, in that the preamp inputs in these cases, have no ground reference, being connected between the inverting and non-inverting inputs.

I don't think there would be a problem with such connection, actually, I've seen an article that suggest this kind of connection to be used with differential preamp to activate a guitar. Here's a link, it's in Russian, though you can take a look at diagrams closer to end of the article. There's also an interesting scheme with active tone controls.

In practice, this will require an additional pole on your series-parallel switch, and the use of the unused lug adjacent to the inverting input connection, on the 4PDT switch.

Don't want to alter the look of the guitar too much, so no additional switches for me (except for the 4PDT one). If the active parallel mode won't indeed work correctly, so be it.

Thanks again for your help!

[fleepd]

Here's a corrected version after mikecg comments

[Yogi B]

Feb 24, 2024 8:57:34 GMT -5 fleepd said:

Feb 24, 2024 8:06:01 GMT -5 mikecg said:

There may be a problem with series active position 5, and all the parallel active positions, in that the preamp inputs in these cases, have no ground reference, being connected between the inverting and non-inverting inputs.

I don't think there would be a problem with such connection, actually, I've seen an article that suggest this kind of connection to be used with differential preamp to activate a guitar. Here's a link, it's in Russian, though you can take a look at diagrams closer to end of the article.

A difference there is that the pickups are DC coupled to the preamp, that's also what I've seen with old Carvin preamps e.g. A500-B3 Bass Preamp, but I'm not sure the difference is significant. The more important thing is that the actual preamp inputs still have a DC path for their bias current.

---

I do have other concerns regarding the preamp design — quoting bajaman's OP:

Aug 25, 2021 17:19:20 GMT -5 bajaman@FSB said:

Winding back the volume control does not wind back the top end response like a passive guitar setup, and you can run any length of instrument cable without losing treble because the pre-amplifier removes the effect of increasing cable capacitance interacting with the pickups top end resonance as it does in a passive system.

This is misleading and only half true.

In a passive system, as the volume control is reduced the pickups are increasingly isolated from the cable capacitance. This can be observed by the fact that at very low volumes the resonant peak of a pickup is at a higher frequency than at maximum volume. So, if that is the case, what causes the treble reduction as the volume is rolled back? Well it is still the cable capacitance, but not due to interaction with the pickup, rather it is interaction with the extra resistance that the volume control introduces. For example, if we assume negligible source impedance from the output of the preamp before the volume control, then the maximum output impedance after a 500k volume control is 125k (= 250k || 250k, i.e. when the resistances from the wiper to the outer terminals of the pot are equal, at 50% on a linear pot or around 80% on a standard log pot). Combining this with the standard 470pF load that approximates a typical 10 foot cable we get a low pass filter with a cut off frequency of 2.7kHz which will likely be quite noticeable (keep in mind that because the pickups are isolated from cable capacitance by the preamp their resonant frequencies will be significantly higher than normal, and thus be above than that 2.7kHz value). The way other active systems avoid the cable capacitance issue is to use low value potentiometers (e.g. 25k), obviously if your intent is to use the same volume for both active & passive modes this is not an option available to you.

On the other hand, presuming you did wrangle a second volume pot (either as a completely separate control, or by modding a dual-gang pot to have different resistances for each half): for a class-A output stage, lower quiescent current equates to diminished capability to drive heavy (low impedance) loads. Thus, the ultra-low current design may preclude the use of such a low value potentiometer anyway.

---

In a later post, bajaman writes:

Aug 28, 2021 23:31:49 GMT -5 bajaman@FSB said:

I simulated the non inverting response with the inverting input grounded and adjusted the input impedance for critical damping - +6dB gain
then i simulated the inverting input, again adjusting the input impedance to damp the coil resonant peak - +6dB gain
then I simulated the preamp in full differential mode and - +12dB gain, BUT, the output response clearly showed that the inverting input coil was being overdamped causing a droop in response of around -7.5dB @ 8kHz relative to midband gain ! So, i readjusted the R3 and R4 resistor values upward (about 10%) until the droop was no longer visible and the output response was now-3dB down @8khz with a smooth rolloff above this frequency

The above account is incongruous to the resistor values presented in the schematic attached to the same post. Those are: R1 = 56k, R2 = 100k, R3 = 270k & R4 = 560k. If you do simulate the circuit with those values you will find that there is still a "droop" (or notch) at 8kHz in the non-inverting response. Additionally, you'll also find that the inverting response has a resonant peak — admittedly a relatively small one at only around 2dB, but nevertheless is therefore underdamped if the objective is to obtain the flattest possible response. Dividing the values of R3 & R4 by 1.1 (in order to undo the described 10% increase) does very little to change either of these outcomes.

Now, for a simple non-differential amplifier I agree with the amount of loading on the 1^st coil is about right (R1 + R2 = 156k), however that's obviously not the setup we have here. I don't know if at some point there was a transcription error for the value of R3 or R4 which then proliferated an incorrect value for the other resistor of that pair. The reason I suspect this is that the correct amount of damping for the 2^nd coil is achieved at around R3 = 170k, which in turn makes R4 = 360k. Although, despite being possible, it would be difficult to reconcile that version of events with the story we've been told.

For me the easiest way to conceptualise why the notch exists, and why only in the non-inverting response, is via a little bit of complex analysis.

Whatever is connected to the inverting input of a differential amplifier forms part of a voltage divider along with R3 & R4 that controls the amount of negative feedback. Thus, the gain of the amplifier is dependent not only upon R3 & R4 but the impedance of the pickup connected to the inverting input. Specifically, the gain applied to the inverting input is inversely proportional to the impedance of the 2_nd humbucker coil plus R3. Because of this inversely proportional relationship, poles in the pickup's impedance (those being the complex frequencies at which the admittance — the reciprocal of impedance — becomes zero) become zeros in the gain at the same frequencies. There is no notch in the inverting response, however, because the exact same poles as are present in the pickup's impedance can be found in its voltage output, thus when that voltage is multiplied by the gain the zeros and poles overlap perfectly and cancel out.

Whereas, in the non-inverting case, the gain is one minus the inverting gain (keeping in mind that the inverting gain has a negative sign, whereas non-inverting gain does not). This additional one makes the points that were previously zeros now become 'ones', shifting the actual zeros into new locations. This means that even if we had identical pickups connected to both inputs and the loading on them was equal (i.e. R1 + R2 = R3), the poles in the voltage applied to the non-inverting input would not align with the zeros in the gain, the two would not cancel, resulting in a notch in the output.

If that's so, what's to be done, how can we eliminate the notch? Continuing the assumption that we have two identical pickup coils: both with (Thévenin equivalent) voltage (V_P) and impedance (Z_P), but with the exception that the coil connected the inverting input is reversed such that its voltage is negative. The voltages that each half of the differential amplifier contribute to the output (V₋ & V₊, for the inverting & non-inverting, respectively) are then given by:
\begin{aligned}
V_- &= -(-V_P) \times \frac{R_4}{R_3 + Z_P}
\\[5ex]
V_+ &= Vp \times \frac{R_2}{R_1 + R_2 + Z_P} \times \left( 1 - \frac{V_-}{-V_P} \right)
\\[3ex]
&= Vp \times \frac{R_2}{R_1 + R_2 + Z_P} \times \left( 1 - - \frac{R_4}{R_3 + Z_P} \right)
\\[3ex]
&= Vp \times \frac{R_2}{R_1 + R_2 + Z_P} \times \frac{(R_3 + Z_P) + R_4}{R_3 + Z_P}
\\[3ex]
&= Vp \times \frac{R_2 (R_3 + R_4 + Z_P)}{(R_1 + R_2 + Z_P)(R_3 + Z_P)}
\end{aligned}From the above it ought to be fairly obvious that if we want V₋ & V₊ to be equal for arbitrary values of Z_P we must set R1 = R3 and R2 = R4, which is what you'll find in virtually any other differential amplifier schematic.

But what if the pickups are dissimilar? In that case you have to go through the process of matching poles & zeros, but assuming the coils aren't too dissimilar the above should still give reasonable results or at the very least make for a good starting point. For bajaman's coils I've already mentioned R3 = 170k and R4 = 360k, but for the others I get R1 = 155k and R2 = 328k (assuming an ideal op-amp) — so R1 & R2 are smaller but only by about 8%, rather than 80% as were the original values. For an exact match, a little extra capacitance (3.3pF) is required to be added in parallel with the first coil; however that's so small that it is likely negligible compared to other sources of stray capacitance within an actual guitar.

---

Based on the values given & what bajaman says, it seems the pickups paired with this variant of the preamp are those used in previous EMG preamp experiments, namely: 8000 turns of .050mm (= 44AWG) wire per coil onto traditional humbucker hardware. The 3-part circuits used as stand-ins for these pickups fail to account for a considerable amount of intrinsic damping, therefore have an extremely high Q-factor, both equal to 24.4, which results in a resonant peak that is much larger than any typical real-world pickup. For reference: an unloaded AlNiCo single coil has a Q that maxes out at around 10; whereas for a pickup with steel pole-pieces the Q will be less (because of increased eddy currents), maybe up to a maximum of around 4 for a uncovered low-wind PAF replica.

If we look at something closer to bajaman's "high output" coils, such as a Seymour Duncan JB (which is still a little underwound in comparison, having a per coil inductance of around 3.5H, purportedly from between 6500—7000 turns of wire): taking a very rough estimate from antigua's plots I get a value of 2.9 for Q. So, if you were to use resistor values based upon calculations involving the 3-part pickup equivalent circuits — with the aim of applying perfect damping in order to obtain as flat response as possible — even though they are supposedly comparable, the real-life version of the pickups will very likely be overdamped by those resistor values (resulting in reduced treble response).

---

In your design where you'll be switching which coils are connected to the preamp, combining coils from disparate pickups (especially if your single coils have AlNiCo pole pieces & your humbucker has steel) it'll be basically impossible to use a single set of resistors that adequately damps both selected coils such that you do not get notches nor resonant peaks.

The first problem, the notches, is the only one of the two that's obviously fixable to me without the need of even more additional switching. The simplest way of doing so is to buffer the inverting input so as to isolate the impedance of the pickup from the feedback divider removing its influence upon the gain of the amplifier.

Buffering the inverting input also makes it possible to add a damping resistor for the second coil that can be adjusted independently, rather than requiring changes to all four of R1—4. However, that still doesn't help the fact that this damping resistor (as well as R1 + R2) should be different for different pickups if your goal really is to have a flat response in each active position.

[mikecg]

Hello again fleepd,

I've had a stab at simulating the 'Baja' pre-amp with a 4 H, 8 k Ohm, 90 pF (nominal humbucker values) pickup connected between the inverting and non-inverting inputs.


This is the circuit I''ve used:

SPOILER: Click to show

And here's a plot of the circuit's frequency response and common mode rejection (CMR). I noticed that with the original values for C3 and R8, the CMR at the lower frequencies, where it matters, was not optimized, so I have had a go at improving it, as you can see in the plot. However, this improvement comes with a slightly impaired low frequency response, but probably not noticeable with normal guitar frequencies:

SPOILER: Click to show

So, my concerns about a 'floating' source appear to be unfounded, and you will not need to provide a ground referenced source in this case.  

[fleepd]

Hello Yogi B, thanks for the very insightful response, i think it will take some time before I can fully grasp it.

Buffering the inverting input also makes it possible to add a damping resistor for the second coil that can be adjusted independently, rather than requiring changes to all four of R1—4. However, that still doesn't help the fact that this damping resistor (as well as R1 + R2) should be different for different pickups if your goal really is to have a flat response in each active position.

Can you elaborate a bit on buffering the inverting input, is it like adding another common collector stage or do you have something else in mind? Also I guess my goal is to have a flat response for humbucker coils with resistors values chosen to match that, and just try my luck with other combinations of pickups.


Hello again mikecg, thanks for this simulation. Its weird CMR was not optimised, but with your values it looks much better.

[mikecg]

Hello fleepd,

I have just updated my 'baja' pre-amp simulation, and the circuit and plot as shown above have been replaced with the updated versions.
The problem with the old version was that my input coupling transformer was configured with a primary:seconday ratio of 1:1 (primary and secondary=4H), and coupling factor of 1. This, coupled with the very low internal resistance of the sine source generator presented a significant load on the secondary circuit, i.e. a  highly overdamped, and low gain response in the secondary coupled circuit.
I have now altered the transformer settings to minimize this primary loading, by setting the coupling factor to 0.5%, and compensating for the resultant amplitude loss in the secondary circuit by reducing the primary inductance to 20 uH. 
The next 'problem' with the old circuit was that I had not included the 'typical' capacitive and resistive loads of 470 pF and 200 k Ohms, and these have now been added.
The differential gain in the passband is now correct, at the specified 12 dB, and there is now a 'typical' humbucker peak in the response of ~ 3 dB at ~ 3.2 kHz.
The CMR plots have also been updated in line with the circuit mods, and once again, best CMR at low frequency is obtained with C3=22 nF, and R8=300k Ohm.
Also included, is an additional 470 pF at the preamp output, to simulate the capacitive load presented by a typical guitar lead.
 

[mikecg]

Hello fleepd,

One final edit!

I've ditched the transformer coupled waveform source in favour of a simpler, and more conventional floating voltage source.
The circuit and plots shown above have been updated.
Differential gain in the passband is confirmed at the specified 12 dB, and the plots are close to identical to the previous edition.
I have included an additional plot showing the amplitude of the partially unloaded resonant peak, without the additional damping resistor (R15=200k).
The value of C5 is not critical - I have set it to 500 pF, to simulate the typical capacitance of a humbucker pickup in parallel with a typical 10' guitar cable.

[Yogi B]

Feb 24, 2024 13:09:46 GMT -5 fleepd said:

Can you elaborate a bit on buffering the inverting input, is it like adding another common collector stage or do you have something else in mind?

That was what I was thinking, yes.

Also I guess my goal is to have a flat response for humbucker coils with resistors values chosen to match that, and just try my luck with other combinations of pickups.

It would help to have the specs of that humbucker.

Feb 25, 2024 8:53:29 GMT -5 mikecg said:

Differential gain in the passband is confirmed at the specified 12 dB, and the plots are close to identical to the previous edition.
I have included an additional plot showing the amplitude of the partially unloaded resonant peak, without the additional damping resistor (R15=200k).
The value of C5 is not critical - I have set it to 500 pF, to simulate the typical capacitance of a humbucker pickup in parallel with a typical 10' guitar cable.

As I understand it the aim of bajaman's preamp is for a full-width flat response, or at least as far as possible (i.e. up to the unloaded resonant frequency). In regard to your latest simulation, you might try:

C5	Delete
R15	Delete
R9	151k
R2	312k
R8	147k
R6	316k
C1	10μ
C3	100n
C4	100n

Additionally, since the plots you've labelled as CMR are negative I'm assuming they're actually common mode gain which isn't necessarily that informative. If we were to replace say R11 with a dead short to ground, the result would be a preamp with a common mode gain of 0 (-∞dB), but also a differential gain of the same. A better metric is therefore the CMRR (common mode rejection ratio), the differential gain divided by common mode gain (then converted to decibels).

Whatever CMRR numbers we do end up with that will of course be a best case scenario, assuming exact component values & matched transistors, in addition to matched pickup coils.

[mikecg]

Hello Yogi B,

My apologies for the delay in replying, as I have, amongst other things, been looking at some alternatives to the 'Baja' pre-amp design, including replacing the two transistors in the 'long tailed pair' with JFET's, and moving away from a discrete design by using a 'micropower' instrumentation amp, namely the AD623, or AD627.

Your suggested mods to the 'Baja' design, appear to be spot on - if simulations are believable, but I am old enough to remember the 'sage' of the 'Electronic Design' journal, Bob Pease's dire warning - "Spice (sometimes) lies"!  

So, without further ado, here are the results of my simulation using your mods, plus one of my own:

The circuit now looks like this:

SPOILER: Click to show

And here are the plots of differential gain, common mode gain, and CMRR:

SPOILER: Click to show

SPOILER: Click to show

SPOILER: Click to show

You may notice that I have reduced the value of R10 from 150 k to 68 k, and 'tweaked' the value of R6 to re-optimize the CMRR.

With R10=150 k, un-distorted peak sine output at 1 kHz is limited to ~ 2.4 V for 0.6 V at the input, with the load as shown, and with no load, this becomes ~ 3.0 V for 0.75 V at the input. It is clear that with R10=150 k, there is not enough 'sink' current to drive the load as shown. With  R10=68 k, un-distorted peak sine output at 1 kHz returns to ~ 3.0 V for 0.75 V at the input, with the load as shown. The downside is that quiescent current increases from ~ 50 uA to ~ 100 uA, but bear in mind that a 500 mAh PP3 battery will still last ~ 208 days, with continuous use! Adding a simple output buffer would probably be a worthwhile, additional mod.  

[mikecg]

In the game of Tennis, there is much talk of 'unforced' errors, so I guess these must be more interesting than 'forced' errors?

Anyway - in dutifully following Yogi B 's instruction to "delete C5", I have definitely made an error, of some sort, in that I should have replaced it with a typical series connected humbucker value of ~ 100 pF.

I will re-run the simulation with C5=100 pF, and update the circuit and plots, in an hour or two.

[mikecg]

Update completed.

[Yogi B]

Feb 29, 2024 11:47:53 GMT -5 mikecg said:

been looking at some alternatives ... using a 'micropower' instrumentation amp, namely the AD623, or AD627

The AD623 is 'low power' rather than 'micropower', with a typical quiescent current of around 300μA.

The AD627 is better with a 85μA maximum, however that has an issue that its minimum gain is 5, or 10 with differential inputs (= 20dB). Furthermore, it has a relatively poor slew-rate of 50mV/μs: about 30% of an LM4250 @ 9V (which still might not be enough, or at least is supposedly a contributing factor for why people run their EMGs at 18V).

Those do appear to be the only two through-hole options, but if that isn't an issue I'd probably be looking at the AD8420.

It is clear that with R10=150 k, there is not enough 'sink' current to drive the load as shown.

I wasn't worrying about that quite yet. With real (lower Q) pickups I'd guess the resistor values would be at least double, so we'd be back above the 560k value bajaman originally had for R6.

Adding a simple output buffer would probably be a worthwhile, additional mod.

I don't really know if there's an advantage of that over just (further) reducing R10.

Feb 29, 2024 16:45:19 GMT -5 mikecg said:

I will re-run the simulation with C5=100 pF

That's equivalent to each pickup having a capacitance of 200pF!

Assuming the voltage output of each pickup is equal & opposite, twice as much current flows through an impedance connected between them as would through the same impedance connected to ground.

(Also, I was working with 90pF — rather than 100pF — since that's what you said previously.)

[fleepd]

Hello mikecg and Yogi B, i see you've made a great progress with the preamp, and thanks a lot for your help.

Feb 29, 2024 0:42:31 GMT -5 Yogi B said:

It would help to have the specs of that humbucker.

That is an excellent question. Of course I knew manufacturer and model, its pretty easy to measure DC resistance, but other than that, I knew basically nothing about the pickup. So for the past few days I've been looking for a way to measure pickup characteristics, and found this thread. It suggests to use an audio interface and a pretty simple device to measure pickup impedance and estimate electrical parameters of a pickup model. So, I've built this device and started testing it.

First, I decided to verify that measuring pickup impedance this way can be trusted. The neck pickup in my guitar is Suhr V60LP and luckily, antigua has measured it, and model parameters can be found in GuitarFreak spreadsheet. So, here's a comparison between antigua measurements and my measurements using Gitec PickupWizard software:




It should be noted that this pickup was measured in circuit, and I didn't know the exact value of volume pot and used approximate value of 250K, but I think the results are surprisingly similar. So then I measured the humbucker, which is Suhr SSH+, here are the results (unloaded and loaded with typical load of 200K/470pF):






Also, pickup model parameters estimated by Gitec PickupWizard software:




The model is slightly different from 6-component model used by JohnH in GuitarFreak spreadsheet:




So, using this model and estimated parameters the simulated preamp response and CMMR is:






In my schematic there's also a slight change in values of voltage divider and placement of the capacitor C1, that is because I tested the circuit on a breadboard with inverting input grounded, and when the circuit is turned on, there's an audible effect of capacitor charging through the voltage divider, and because this preamp is supposed to turned off and on, this effect is undesirable. 

So, what do you think of these changes, and any thoughts, comments, ideas would be appreciated.

[mikecg]

Hello again fleepd, 

You seem to be making good progress with your project, and the comparison of your pickup measurements with antigua 's data shows that you are on the right track.

However, my initial 'take' on the 'Baja' preamp was not adequately informed, and so I have spent some time re-reading the source material, and also Yogi B 's analysis, and it is now clear to me that the 'Baja design is not the 'right tool for the job'.

As you may well already know, you are proposing to construct two thirds of a (very basic) op-amp, consisting of an input stage, a gain stage, and in this case, no push-pull output stage. Ideally, the circuit should have a differential gain of 12dB (x4), and input impedance(s) independently adjusted to achieve critical damping of the pickup signals from the inverting and non-inverting inputs. In addition, it was originally envisaged that it would be capable of driving a load consisting of a standard guitar volume control (500k or 250k) in parallel with a standard guitar cable (470pF) and a guitar amplifier with a (resistive) input impedance of 200k.
Yogi B 's analysis shows that even a single (whole) op-amp - let alone a 'Baja (part) op-amp - will not 'cut it' - no matter how it is configured.

But I hasten to add, that all is not lost!

Your preamp requirement appears to be a perfect fit for what is known in 'the trade' as an 'instrumentation amp', typically consisting of three opamps, so more complex, than the 'Baja' design, but probably just as easy to construct.

I have two designs in mind, one based on the classic three opamp configuration, using the opamp that Yogi B mentioned, the LM4250 (x3), or LM4250 (x2) + OPA703 (x1), and the other based on a fully integrated low power device, the AD623.

These preamps have about the same specs, 12dB differential gain, independently adjustable (resistive) input impedance(s), 1v peak sine input, for 4v peak sine output in a 100Hz to 10kHz passband, and quiescent current in the range 170 to 270 uA.
A good 'standard' PP3 battery will have a capacity of up to ~ 700mAh at a 1mA rate, so battery life for the 270uA design should pan out at something like 324 days at 8 hours a day - plenty long enough - I think!
The other advantage worth mentioning is that the higher current draw designs can output a minimally distorted 8 v peak to peak (100Hz - 10kHz) into a load consisting of a 25k pot in parallel with a standard cable and amp, minimizing the effects of guitar cable capacitance on volume control setting.

If you would like me to provide further details of these designs, I will gladly oblige - but if not - well - no harm done    

[fleepd]

Hello mikecg, yes, this sounds really interesting and I definitely would like further details.

[mikecg]

Hello again fleepd,

Well - it looks like I may have to 'eat my words', as a single opamp may well 'cut it' - after all!

But not just any old opamp - and definitely not the Baja kind. 

The following design was inspired by Yogi B 's suggestion that the 'problem' with the inverting input on the 'standard' diff. opamp could be solved by buffering it, and of course, that idea forms the genesis of the classic three opamp instrumentation amp. But how about a simpler solution with just one opamp? 
Turns out that if you can configure the basic circuit with high enough impedances, the effect on closed loop gain of the change in source impedance at, or near resonance, can be minimized. However, this strategy requires a certain type of opamp, primarily, one with a very low input bias current, decent gain bandwidth product, slew rate, stable operation at low closed loop gain, 'rail to rail' input and output specs. and very low current consumption from a 9 volt battery supply. In addition, it should be in production, cheap to buy, and available in the through hole pdip format. Luckily, there are candidates that meet most, if not all of this long list of requirements, and the OPA703 rides to the rescue!

So, with the old adage that 'simple is best', in mind (especially if you are just starting out on a journey of 'electronic exploration'), here is a simple circuit that should meet with your requirements. I strongly suggest that you try this one first - if for some unforeseen reason this proves to be unsuitable, then a design using an AD623, would probably be my next best suggestion:

Here's the circuit diagram for the OPA703 preamp that includes your pickup data:

SPOILER: Click to show

Note that for the above circuit simulation, the pickup coils are ground referenced, with the 'slug coil' connected in 'reverse polarity', and this means that 'hum' signals for both amp inputs will be 'in phase', and therefore subject to the common mode rejection facility provided by the differential configuration of the opamp circuit, whereas string signals from the pickup coils are in anti-phase and will be summed and amplified. Due to the balanced nature of the inputs to the differential amp, pickups can either be ground referenced, or by connecting the nodes labelled 'white' and 'red' together, can function as a 'floating' input, as is required for this particular application.


And here's the gain plots:

SPOILER: Click to show

And the CMMR plot with the pickup model included:

SPOILER: Click to show

Next up is the circuit I've used to simulate the 'amp only' CMMR, and the large signal transient response, the power bandwidth, and slew rate limit:

SPOILER: Click to show

And here's the large signal transient plot:

SPOILER: Click to show

And finally the 'amp only' CMRR plot:

SPOILER: Click to show

Quite promising, I think you will agree. One word of warning when you come to layout the design on stripboard or similar, stray capacitance can cause problems especially when you have high value resistors in circuit, so try to minimize 'board' capacitance across the feedback resistor. The simulation shows that a 2 pF capacitor in parallel with the 2 megohm feedback resistor is optimal, and a convenient way to implement small adjustable capacitors is to take two short lengths of ~ 40 gauge enamelled wire, strip the enamel from one end of each wire, and use those ends as the terminals of your trimmer capacitor. Once you have the two wires soldered to your board, twist them together - more twists = more capacitance.

[Yogi B]

Mar 3, 2024 11:04:43 GMT -5 fleepd said:

The model is slightly different from 6-component model used by JohnH in GuitarFreak spreadsheet]

Yeah, and it does the thing that irks me whereby there is a frequency dependency embedded in a source — rather than being expressed as separate impedance(s).

It also means you can't just swap in a constant (frequency independent) voltage source for the current source, instead it should have a voltage given by V = I Z_c (where Z_c is as defined in the PickupWizard docs: the sum impedance of the parallel resistances & inductances to the left of the current source).

If we assume k_v v₀ = 1 so as to get a 'flat' ('integrated') response equalling 0dB at 0Hz, and assume that the calculated values of R₂ are so large they may as well be infinite, it can then be shown that the voltage across the current source is given by:
V = \frac{R_1 + \dfrac{s}{\frac{1}{L_1} + \frac{1}{L_2}}}{R_1 + s L_1}Here there are two important things to recognise: first is that the above expression takes the form of a low pass shelving filter; second is that R₁ & L₁ already form two thirds of such a filter. The final third to complete the filter is the addition of another resistor (R_G) connected between ground and the junction between L₁ & L₂.

Equating the newly formed voltage divider with the above voltage and allowing a new value (R_P) for R₁ (such that R_P & R_G in parallel equals R₁, so that the total impedance remains unchanged), we arrive at the following:
\begin{aligned}
R_P &= \frac{L_1 + L_2}{L_2} R_1
\\[2ex]
R_G &= \frac{L_1 + L_2}{L_1} R_1
\end{aligned}With the below circuit:

---

In my schematic there's also a slight change in values of voltage divider and placement of the capacitor C1, that is because I tested the circuit on a breadboard with inverting input grounded, and when the circuit is turned on, there's an audible effect of capacitor charging through the voltage divider, and because this preamp is supposed to turned off and on, this effect is undesirable.

Generally (and what you've shown in previous diagrams) the preamp is switched in/out of the audio path, but remains powered even when disengaged (and therefore the cap(s) remain charged).

---

Mar 8, 2024 18:27:21 GMT -5 mikecg said:

Turns out that if you can configure the basic circuit with high enough impedances, the effect on closed loop gain of the change in source impedance at, or near resonance, can be minimized.

The disadvantage of adding large resistances in series with the signal is you add in their thermal noise. A voltage divider formed by 1 & 2 megohm resistors has a voltage noise density of 105 nV/√Hz, more than twice the 45 nV/√Hz value of the OPA703 @ 1kHz. Although the value for the op-amp does become larger at lower frequencies that's of relatively little importance — it should be fairly obvious as to why from the use of frequency (rather than octaves or decades), in the units.

I should also say that 45 nV/√Hz isn't too great in the grand scheme of things: the resistance of the humbucker coils themselves set the thermal noise floor (of around 17 nV/√Hz, though the neck & middle single coils will be lower at approx. 10 nV/√Hz) and in an ideal world we'd want to keep at that level or lower for the rest of the components. Despite being difficult to achieve that with the selection of op-amps limited to meet the given requirements, it seems silly to commit worse transgressions with something we do have more control over (resistor values).

The following design was inspired by Yogi B's suggestion that the 'problem' with the inverting input on the 'standard' diff. opamp could be solved by buffering it, and of course, that idea forms the genesis of the classic three opamp instrumentation amp. But how about a simpler solution with just one opamp?

If using two op-amps, I wouldn't use one to just buffer the inverting input: I'd use it with a gain of two. That way we can lose the voltage divider on the non-inverting input of the second op-amp (the one wired as the differential amp), and use equal values for the negative feedback divider to give a non-inverting gain of 2 and inverting gain of 1 (the latter signal having already been doubled by the first op-amp).

[mikecg]

Hello again Yogi B,

Thanks for your continuing contributions to this thread. I take your point about resistor noise, and if this was part of a Hi-Fi set-up, I would of course avoid using such high values. My circuit simulation suggests that an average value for the spectral noise density at the pre-amp output in the 1 kHz to 10 kHz frequency range may be ~ 450 nV/√Hz, and so I would expect the noise at the pre-amp output to be ~ 45 uV RMS.
Dare I say, still at a tolerable level, when compared to other (E-M) noise sources normally associated with guitar pickup operation in the 'real world'. 

[mikecg]

Hello fleepd,

I hope you are making some progress with your project.

As Yogi B has already mentioned, the single opamp circuit suffers from two weaknesses; closed loop gain is dependent on input impedance, and my attempt to minimize this dependency, by introducing high value resistors, increases circuit noise. The next step-up in complexity is the classic two opamp circuit configuration, that removes the closed loop gain dependency, and the need for very high value (noisy) resistors. Details can be found in the following links:

www.analog.com/media/en/training-seminars/tutorials/MT-062.pdf


www.ti.com/lit/an/sboa281/sboa281.pdf?ts=1691103689365&ref_url=https%253A%252F%252Fduckduckgo.com%252F


And here's the circuit, configured for a differential gain of x4, with your pickup model attached:

SPOILER: Click to show

Simulations have been made using two LM4250 'programmable' opamps, operating at various 'bias' currents, and also using two OPA703 (non-programmable) opamps.

And here's a tabulated summary of some data based on the results provided by the circuit simulation(s):

SPOILER: Click to show

Note that the battery life data are based on a 'pro' quality 9 V PP3 size, with a stated capacity of ~ 700 mAh, such as the Procell 'Constant', as shown here:

www.procell.com/wp-content/uploads/2022/07/Datasheet_Constant_9V_-PC1604_Rev1.pdf