Post by JohnH on Aug 30, 2013 19:43:46 GMT -5
I’ve been wanting to get my head around how best to set up guitars and understand how the various factors interrelate. So I’ve made this spreadsheet to work out the theoretical amount of compensation at the bridge, based on all the various parameters. This includes string gauge and type, tuning frequency, scale length, action height, neck relief and nut height.
To do this, I used a formula that relates string tension, frequency, length and mass, and combined that with what I know about stress and strain, and how when a string is depressed, the extra length required will stretch it slightly more, adding tension and so raising its pitch.
The spreadsheet is here:
Stringtheory1.1
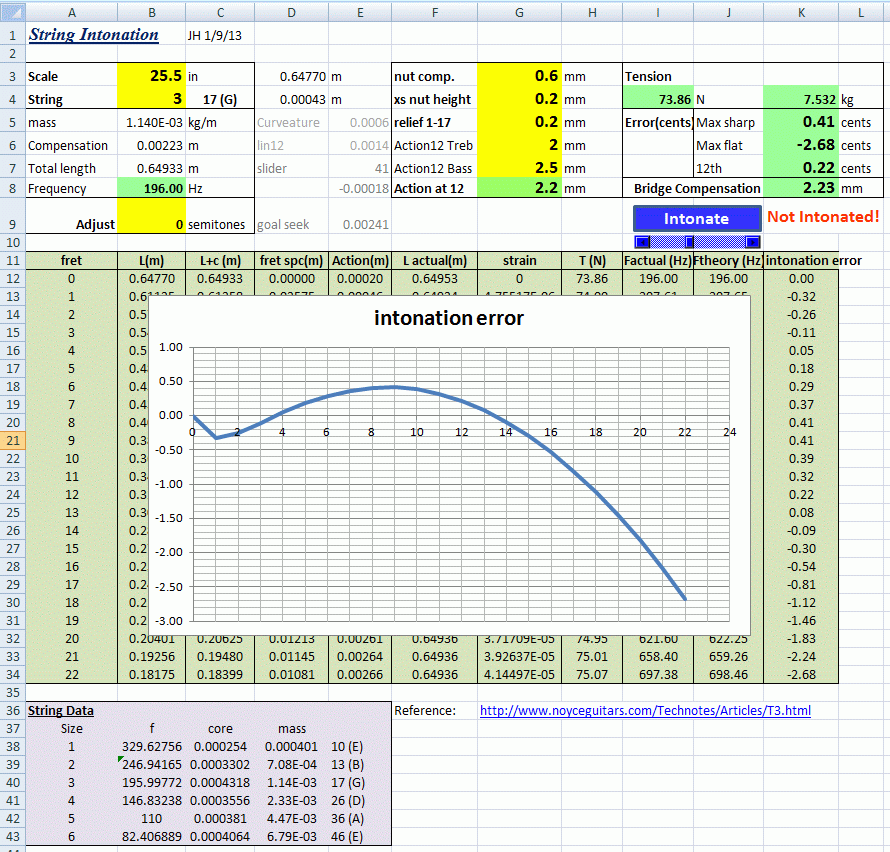
Inputs are in yellow cells, results are green, showing string tension, the amount of compensation in terms of added length at the bridge, and a graph of how intonation will vary at each fret, once adjusted for correct open tuning, and compensation based on the 2nd harmonic and 12th fret.
Scale length is input in inches, but all the maths is in metric SI units (it’s the only way to make physics work properly!). The strings are entered as numbers 1 to 6. This calls up data from a table for diameter, mass, and the base frequency in standard tuning. Now it would have been nice if all strings were consistent for these parameters, in which case string properties could be calculated. But this is not the case, particularly with wound strings where the shape and diameter of the core, and the weight of the winding wire varies for each brand, and between strings. Even the plain strings are not entirely consistent, since they are both steel, plus coating. So the data here is from the only complete set of info I can find, which is a set of 10-46 strings from Dean Markley, with wound D, A and low E, as described here by Noyce Guitars (which is also a good article for reference):
www.noyceguitars.com/Technotes/Articles/T3.html
So, to operate the spreadsheet: Input the string number and scale length. Then the action you want at the 12th fret, and the neck relief. This is input in terms of what you will probably measure, being the relief measured beneath a straight edge from 1st to 17th fret. 0 is dead straight. This is then converted to an overall curvature of the neck. Finally, the height at the bottom of the neck slot. 0 means the slot is exactly at the depth of a 0 fret, following the profile set up by the other frets. This gives the best result, but if you want it a bit higher so help buzzes, enter it in mm.
Then, press the ‘Intonate’ button, and a goal-seek function will adjust compensation until intonation at the 12th fret is correct. You can now see how the result varies at each fret, with errors shown as cents of a semitone (50cents = ½ semitone – ew!). Im not sure what a perfectly acceptable result would need to be, but I suspect that 10 cents is too much, 5 cents may be OK and 2 cents is good. There is also a slider, to make a further manual adjustment of +/- 1mm. Macros need to be enabled to run these features.
The calculations are based on a perfectly light touch to depress the string down to the fret. Any heavier fretting action will go sharper, but is not captured here.
Observations
So what does this tell us? Here are some conclusions about what may make acceptable intonation easier or more difficult to achieve:
To do this, I used a formula that relates string tension, frequency, length and mass, and combined that with what I know about stress and strain, and how when a string is depressed, the extra length required will stretch it slightly more, adding tension and so raising its pitch.
The spreadsheet is here:
Stringtheory1.1

Inputs are in yellow cells, results are green, showing string tension, the amount of compensation in terms of added length at the bridge, and a graph of how intonation will vary at each fret, once adjusted for correct open tuning, and compensation based on the 2nd harmonic and 12th fret.
Scale length is input in inches, but all the maths is in metric SI units (it’s the only way to make physics work properly!). The strings are entered as numbers 1 to 6. This calls up data from a table for diameter, mass, and the base frequency in standard tuning. Now it would have been nice if all strings were consistent for these parameters, in which case string properties could be calculated. But this is not the case, particularly with wound strings where the shape and diameter of the core, and the weight of the winding wire varies for each brand, and between strings. Even the plain strings are not entirely consistent, since they are both steel, plus coating. So the data here is from the only complete set of info I can find, which is a set of 10-46 strings from Dean Markley, with wound D, A and low E, as described here by Noyce Guitars (which is also a good article for reference):
www.noyceguitars.com/Technotes/Articles/T3.html
So, to operate the spreadsheet: Input the string number and scale length. Then the action you want at the 12th fret, and the neck relief. This is input in terms of what you will probably measure, being the relief measured beneath a straight edge from 1st to 17th fret. 0 is dead straight. This is then converted to an overall curvature of the neck. Finally, the height at the bottom of the neck slot. 0 means the slot is exactly at the depth of a 0 fret, following the profile set up by the other frets. This gives the best result, but if you want it a bit higher so help buzzes, enter it in mm.
Then, press the ‘Intonate’ button, and a goal-seek function will adjust compensation until intonation at the 12th fret is correct. You can now see how the result varies at each fret, with errors shown as cents of a semitone (50cents = ½ semitone – ew!). Im not sure what a perfectly acceptable result would need to be, but I suspect that 10 cents is too much, 5 cents may be OK and 2 cents is good. There is also a slider, to make a further manual adjustment of +/- 1mm. Macros need to be enabled to run these features.
The calculations are based on a perfectly light touch to depress the string down to the fret. Any heavier fretting action will go sharper, but is not captured here.
Observations
So what does this tell us? Here are some conclusions about what may make acceptable intonation easier or more difficult to achieve:
- Shorter scales are trickier than longer scales
- Low fundamental frequencies are harder than higher ones (eg G is more problematic than high E)
- High action and high neck relief makes the problem greater
- A nut that is not cut deep enough makes a big difference in the first few fretted positions, but about 0.1 or 0.2mm excess height is OK
- Wound strings work better than plain strings for intonation
- Drop tuning of a semitone or two doesn’t make too much difference
- High frets 18 and up seem to tend to go flat. Does anyone find this in practice? It may be compensated by fretting pressure and bending
- String weight doesn’t actually make much difference (eg changing from ‘10s’ to ‘11s’). For theoretical strings made of the same material and tuned to the same frequency and same set-up, the compensation is the same. In practice, irregularity between strings and sets makes a small difference.
That’s all for now, I hope that is interesting!
cheers
John
EDIT 2/9/13 Added to version 1.1: Nut compensation, and string action heioght at 12th based on setting treble side and bass side, with linear variation between.