|
|
Post by perfboardpatcher on Apr 9, 2016 3:02:21 GMT -5
This topic is a continuation of "Humbucker as replacement for the dummy coil". Well that's how I planned it, but the response on "Humbucker as replacement for the dummy coil" wasn't that overwhelming  and therefor the following was kept on the shelf for a while. Anyway, in this new topic the humbucker(s) won't be wired anti-series or anti-parallel as in "Humbucker as replacement for the dummy coil" but in series or in parallel and with a 3rd coil "intertwined". As example I will use an HH configuration. So the variations available are: (1) bridge HB (series or parallel) + one coil of the neck HB and (2) neck HB (series or parallel) + one coil of the bridge HB. The 3-coil combinations are kinda twisted, the added 3rd coil is in series with one of the HB coils and in parallel with the other HB coil. The 3rd coil is designated (anti-)series or (anti-)parallel which is based on the "hum-catching"  duo, between parentheses.  Do 3rd coil series and parallel sound noticeably different from series neck and bridge HB together in parallel or bridge and neck single coil together in series? Are there any new sounds in the 3rd coil "anti" combinations? Cheers, Paul |
|
|
|
Post by JohnH on Apr 9, 2016 4:34:02 GMT -5
Hi Paul
For those wondering, yes there are indeed a number of 3-coil humcancelling variants, based on carefully paying attention to polarity and phase. I have them on two of my guitars, including stock o the firs electric I ever had - which I think I posted about before. You seem to have the theory right there, (except (C+D) x D, but we can overlook that one!)
|
|
col
format tables
Posts: 474
Likes: 25
|
Post by col on Apr 9, 2016 19:46:20 GMT -5
Am I understanding this correctly; these are supposed to be him-cancelling arrangements - yes? Unless I'm mistaken, don't the coil arrangements need to be matched!?
So, you could have the following (hum-cancelling) arrangements:
AxD
A+D
BxC
B+C
(AxD)+(BxC)
(A+D)x(B+C)
Ax(-C)
A+(-C)
Bx(-D)
B+(-D)
(Ax(-C))+(Bx(-D))
(A+(-C))x(B+(-D))
The above examples assume identical pickups for full hum-cancelling effects. But maybe there is something I am missing about hum-cancelling theory.
|
|
|
|
Post by JohnH on Apr 9, 2016 20:30:17 GMT -5
Col - yes there really are fully humcancelling combos of three coils, assumed similar except for polarity.
eg, for a combo sounding in phase, First, put two south coils in series. That creates a combined result with twice the hum, but also twice the impedance. Put that group in parallel with one north coil, which has -1 x hum and 1x impedance. The net result is zero hum because of the combination of hum from the two south coils, but with greater impedance, balances the lesser hum, with lesser impedance fro the north. The analysis of that is very similar to our discussion of the sound of these hybrid combos, see the current 'does this make a difference?' thread.
What happens is that, due to voltage divider action of the three coil impedances, the output sees 1/3 of the hum generated by each of the two series south coils, which is balanced by 2/3 of the anti-hum from the north coil, to make full hum cancellation.
I know all this is true because two of my guitars do this. In fact it was the surprise of first noticing this effect that got me interested again in guitar electronics about 10 years ago.
|
|
col
format tables
Posts: 474
Likes: 25
|
Post by col on Apr 9, 2016 21:41:19 GMT -5
Hmmm. Interesting. So, the following would be hum-cancelling:
(AxC)+B
What about:
(AxC)+(BxD) ?
If I understand correctly, this too would be hum-cancelling because the second in-series coils (BxD) would then have the same impedance as (AxC). Well, that's to be expected; but tree coil result is a surprise. You know, now that you mention it, it seems like I've long ago read this here but forgot about it until now.
What the situation with:
(A+C)xB ?
I'm supposing that only partially hum-cancels.
|
|
|
|
Post by JohnH on Apr 9, 2016 21:55:25 GMT -5
Hmmm. Interesting. So, the following would be hum-cancelling: (AxC)+B What about: (AxC)+(BxD) ? If I understand correctly, this too would be hum-cancelling because the second in-series coils (BxD) would then have the same impedance as (AxC). Well, that's to be expected; but tree coil result is a surprise. You know, now that you mention it, it seems like I've long ago read this here but forgot about it until now. What the situation with: (A+C)xB ? I'm supposing that only partially hum-cancels. They are all in theory, fully humcancelling. But the last one is more critically dependent on exact balancing of coils, so practical versions of it can have some hum. However,the previous parallel type is largely self compensating for different coil windings. You could even put three south coils in series and have them balance with one parallel north coil. It is also why with two coils, you can mostly hum cancel an M with a hotter wound but otherwise similar B pickup. The extra hum picked up is mitigated by the added impedance. |
|
|
|
Post by perfboardpatcher on Apr 10, 2016 1:51:23 GMT -5
Hi Paul For those wondering, yes there are indeed a number of 3-coil humcancelling variants, based on carefully paying attention to polarity and phase. I have them on two of my guitars, including stock o the firs electric I ever had - which I think I posted about before. You seem to have the theory right there, (except (C+D) x D, but we can overlook that one!) The Shergold, I remember... Nope, it has to be perfect! I have uploaded a new image, thanks for pointing out the error, JohnH. |
|
|
|
Post by Yogi B on Apr 12, 2016 23:38:07 GMT -5
Anyway, in this new topic the humbucker(s) won't be wired anti-series or anti-parallel as in "Humbucker as replacement for the dummy coil" but in series or in parallel and with a 3rd coil "intertwined". I'd say that the notion of separating these into separate topics is flawed -- when I look at a guitar (with the pertinent pickup configuration) I think "four coils" instead of "two humbuckers". The combinations you note as: (A x C) + B (C x A) + D (D x B) + A (B x D) + C (A x ~D) + B (D x ~A) + C (B x ~C) + A (C x ~B) + D (A x ~B) + D (B x ~A) + C (C x ~D) + B (D x ~C) + A can be made to fall under a single grouping (or formula if you like) by thinking all coils are of the same (electrical) polarity in this case making coils B and D already out of phase (i.e. imagine the coils as A, ~B, C, and ~D). for the above that would be: (P x P) + ~P, likewise can be done for the case of the dual yielding: (P + P) x ~P. Thus rather than thinking of the total twenty-four different hum-cancelling-three-coils-out-of-two-humbuckers-active combinations, using a specific set naming convention and polarities, and further divided into two sub-categories across two threads -- we can instead think of two general rules that can be easily applied to any arbitrary set of coils that we might wish to take a selection of three. |
|
|
|
Post by perfboardpatcher on Apr 17, 2016 7:15:36 GMT -5
Hmmm. Interesting. So, the following would be hum-cancelling: (AxC)+B What about: (AxC)+(BxD) ? If I understand correctly, this too would be hum-cancelling because the second in-series coils (BxD) would then have the same impedance as (AxC). Well, that's to be expected; but tree coil result is a surprise. You know, now that you mention it, it seems like I've long ago read this here but forgot about it until now. What the situation with: (A+C)xB ? I'm supposing that only partially hum-cancels. They are all in theory, fully humcancelling. But the last one is more critically dependent on exact balancing of coils, so practical versions of it can have some hum. However,the previous parallel type is largely self compensating for different coil windings. You could even put three south coils in series and have them balance with one parallel north coil. It is also why with two coils, you can mostly hum cancel an M with a hotter wound but otherwise similar B pickup. The extra hum picked up is mitigated by the added impedance. What would be a bad case scenario? Let's say the hot bridge pickup has 2 coils (A,B) with a resistance of 10 kOhms and a hum output of 10 Volts(!) for each coil and the vintage neck pickup has 2 coils (C,D) with a resistance of 5 kOhms and a hum output of 5 Volts for each coil. (A + C) x B -> 10 * 5/15 + 5 * 10/15 - 10 = 100/15 - 10 = 6.667 - 10 = -3.333 Volts. the non-humbucking combo version would give (-)16.667 Volts hum. 16.667 / 3.333 = 5 -> 14.0dB attenuation (C+ A) x D -> 5 * 10/15 + 10 * 5/15 - 5 = 100/15 - 5 = 6.667 - 5 = 1.667 Volts. the non-humbucking combo version would give (-)11.667 Volts hum. 11.667 / 1.667 = 7 -> 16.9dB attenuation |
|
|
|
Post by perfboardpatcher on Apr 17, 2016 8:19:32 GMT -5
Anyway, in this new topic the humbucker(s) won't be wired anti-series or anti-parallel as in "Humbucker as replacement for the dummy coil" but in series or in parallel and with a 3rd coil "intertwined". I'd say that the notion of separating these into separate topics is flawed -- when I look at a guitar (with the pertinent pickup configuration) I think "four coils" instead of "two humbuckers". The combinations you note as: (A x C) + B (C x A) + D (D x B) + A (B x D) + C (A x ~D) + B (D x ~A) + C (B x ~C) + A (C x ~B) + D (A x ~B) + D (B x ~A) + C (C x ~D) + B (D x ~C) + A can be made to fall under a single grouping (or formula if you like) by thinking all coils are of the same (electrical) polarity in this case making coils B and D already out of phase (i.e. imagine the coils as A, ~B, C, and ~D). for the above that would be: (P x P) + ~P, likewise can be done for the case of the dual yielding: (P + P) x ~P. Thus rather than thinking of the total twenty-four different hum-cancelling-three-coils-out-of-two-humbuckers-active combinations, using a specific set naming convention and polarities, and further divided into two sub-categories across two threads -- we can instead think of two general rules that can be easily applied to any arbitrary set of coils that we might wish to take a selection of three. Yogi B, Since "Humbucker as replacement ..." already dealt with certain 3 pup coil combinations I see no reason to include these very same combo's in this topic. I understand what you're saying but the convention on this forum is that the coils are A, B, C and D. In this convention magnet polarity is included. (S=+, N=~ or vice versa.) The coils are A, ~~B, C and ~~D. I have no objections.  |
|
|
|
Post by perfboardpatcher on Apr 18, 2016 13:46:38 GMT -5
I've been playing around with some "tillman" stuff. What I was after was a manner to calculate the eq effect caused by selecting a different pickup combination, for instance (A x C) + B compared to A + B. a. The formula to calculate the relative displacement velocity, V_pup = sin (pi . X_pup . F_string / L_scale . F_open) The calculation is made per pickup, therefor 3 functions f(A), f(B), f(C) . b. Weighted factors for the functions. To take into account the loading of the pickup. See the image below. Weighted factors are: W_A = 1/3, W_B = 2/3, W_C = 1/3, R_A = 1/2, R_B = 1/2, R_C = 0 . Magnet strength or distance between pickup and strings could be factored in as well. 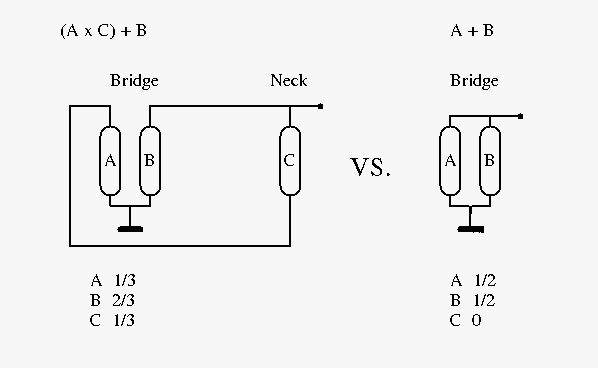 c. (a) and (b) together give the formula to calculate the gain per frequency. A = (W_A * f(A) + W_B * f(B) + W_C * f(C)) / ( R_A * f(A) + R_B * f(B) + R_C * f(C)) Graph plot per string (db/Hz)
The other 5 strings give similar pictures, the graph is being moved to the right every time the string gets thinner. 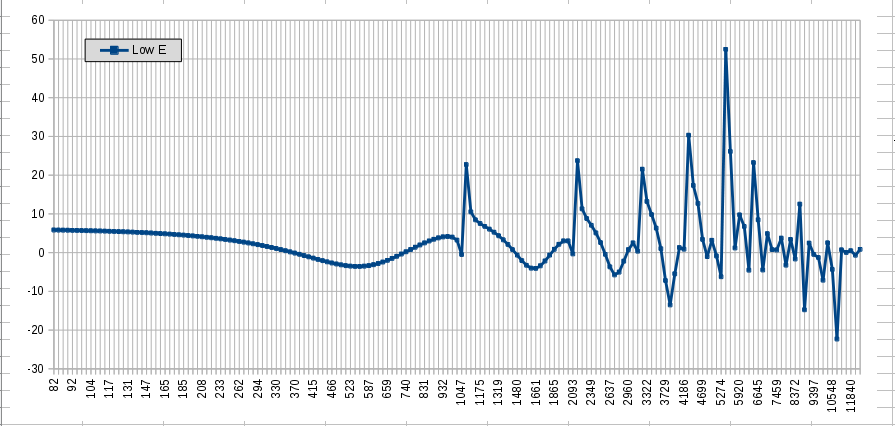 Graph plot for all strings together, chromatic scale in a specific position (db/Hz) Graph plot for all strings together, chromatic scale in a specific position (db/Hz)
For instance, position 0 uses root notes starting from the open E and then F, F#, G, G# and their harmonics on the low E string. Same principle for all the other strings except G for which only 4 notes are used. An average is being calculated for those frequencies with results from more than one string. Not sure what to think of that treble boost... 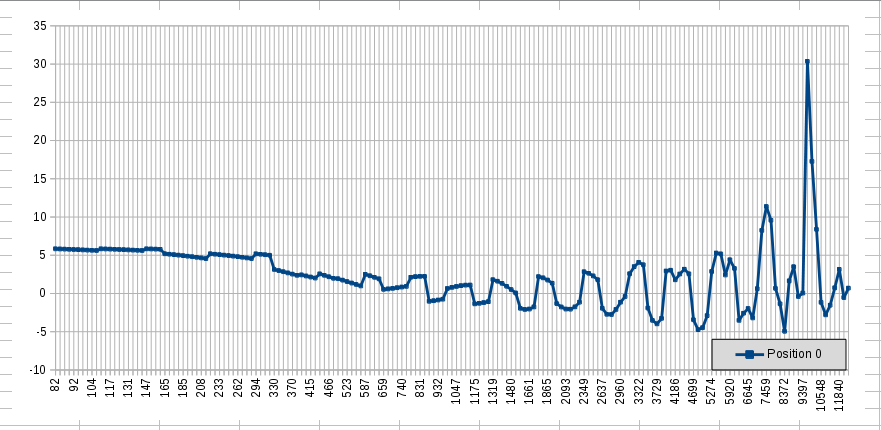 |
|
|
|
Post by JohnH on Apr 18, 2016 17:19:35 GMT -5
Those are interesting plots. But im having trouble relating to them. Eg, for the single string plot, where is the fundamental frequency? What makes that high treble spike?
I built Tillmans theory into GuitarFreak, but I decided that if we are going to add the pickup response to the electrical charactetistics, we also need to know how vibration frequencies of strings vary with higher-frequency harmonics. It turns out you can get quite a valid plot with a 6db per octave roll off after a frequency determined by the fundamental note, the fret position and where you pick.
I watch out on the web for others dabbling in these kind of calcs. Once you get outside of simple electrical modelling of simple guitar circuits, I think it may be down to just you and me dude!
|
|
|
|
Post by Yogi B on Apr 19, 2016 1:40:42 GMT -5
Those are interesting plots. But im having trouble relating to them. Eg, for the single string plot, where is the fundamental frequency? What makes that high treble spike? There aren't any high treble spikes as such, I'm not sure but it sounds like you might be making the same misinterpretation that I was for a couple of hours? The graphs are of the difference between the two settings i.e. V[(AxC)+B] / V[A+B], thus the spikes are caused by the zeros in the response of A+B, similarly the shape of the fundamental is largely quashed because it is common to both. |
|
|
|
Post by perfboardpatcher on Apr 19, 2016 13:42:28 GMT -5
JohnH, What I did was to compare the output of the 3 coil pup combination with the output of the parallel hb. So what the graph tells me is that when I switch from hb to 3 coil combo I get some 6 dB of boost in the low end and some 30 dB of boost at 9673Hz. BTW, I haven't explained yet but there are 24 data points per octave, derived from center frequency A = 110.000Hz. The reason for the treble spike is already explained by Yogi B and I can show it to you in a graph. Referring to (c) of my previous post, if I put the parallel hb (A + B) in the numerator (was in the denominator) and use 1 (straight line) as denominator the graph looks like this:
Parallel HB compared to 1 (straight line)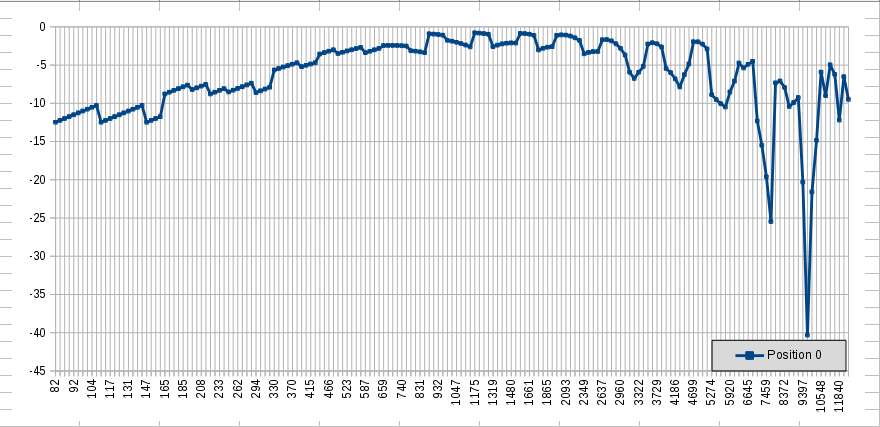 The graph plot shows a valley at 9673 Hz (I looked it up in the table). This harmonic is present on D (fret 72.5) and B string (fret 63.5) but unfortunately at a spot where the comb filters strike! So it makes sense, compared to (A + B) the 3-coil combo (A x C) + B has lots of 9673Hz, relatively speaking. Parallel HB - D string (dB/Hz)
(hb compared to a straight line, should give the same results as the tillman java applets) 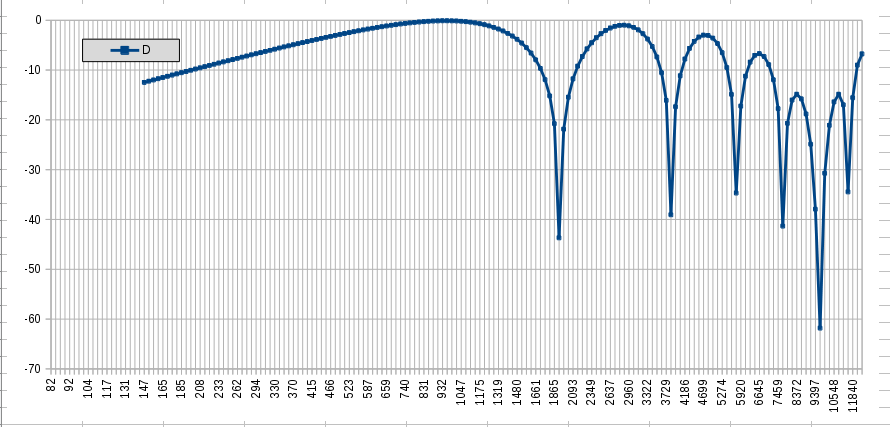 Parallel HB - B string (dB/Hz) Parallel HB - B string (dB/Hz)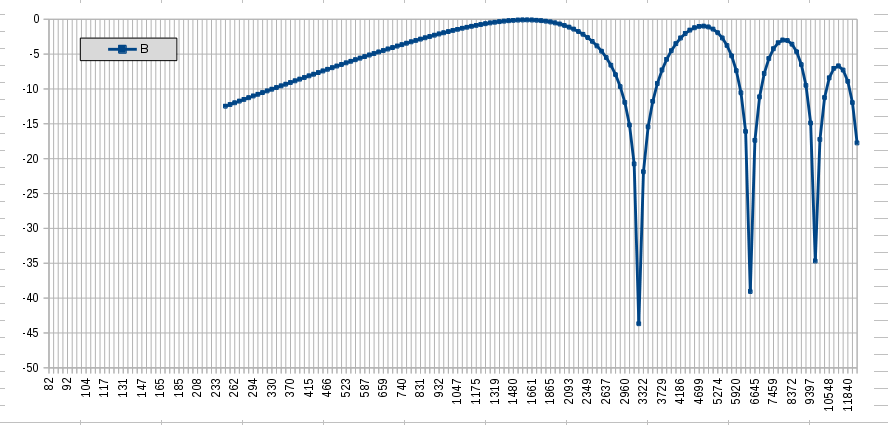 |
|
|
|
Post by JohnH on Apr 19, 2016 17:47:51 GMT -5
Ok thanks, I understand better what you are doing now. A couple more observations:
Why does the (AxC)+B seem to show 6db at low frequencies above the A+B case? Id have expected 20log (4/3) = 2.5db for that. But yes to 6db if it was an (A+B)xC case.
Electric guitars dont have much to say above 5khz. There are several factors in the signal chain from pick to speaker that rolls higher frequencies right down. So a significant result at 9khz may not be so significant in practuce.
Interesting work...
|
|
|
|
Post by perfboardpatcher on Apr 20, 2016 13:33:42 GMT -5
Ok thanks, I understand better what you are doing now. A couple more observations: Why does the (AxC)+B seem to show 6db at low frequencies above the A+B case? Id have expected 20log (4/3) = 2.5db for that. But yes to 6db if it was an (A+B)xC case. Electric guitars dont have much to say above 5khz. There are several factors in the signal chain from pick to speaker that rolls higher frequencies right down. So a significant result at 9khz may not be so significant in practuce. Interesting work... It's true that (AxC)+B delivers more output overall (2.5dB) than A+B. If I use 0.667 as weighted factors for the A+B coils I get a result of 3.3dB,that is boost in the low end. (A+B)xC has almost 12dB more bass than A+B. Perhaps you meant AxB (5.5dB)? |
|
|
|
Post by JohnH on Apr 20, 2016 16:04:44 GMT -5
(A+B)xC has almost 12dB more bass than A+B. Perhaps you meant AxB (5.5dB)? I'll stick with what I wrote thanks, (A+B)xC has 6db ( ie x2 signal voltage) more low end than A+B. |
|
|
|
Post by perfboardpatcher on Apr 23, 2016 2:52:48 GMT -5
(A+B)xC has almost 12dB more bass than A+B. Perhaps you meant AxB (5.5dB)? I'll stick with what I wrote thanks, (A+B)xC has 6db ( ie x2 signal voltage) more low end than A+B. Perhaps were not talking about the same coil B.  If I move my coil B to become a strat mid pup I get 5dB. |
|
|
|
Post by perfboardpatcher on Apr 23, 2016 3:17:56 GMT -5
Some other aspect of selecting another pickup combination, the resonance peak moves up or down, which can also be considered as an eq effect. In case of (A+B) -> (AxC)+B, a rough calculation: 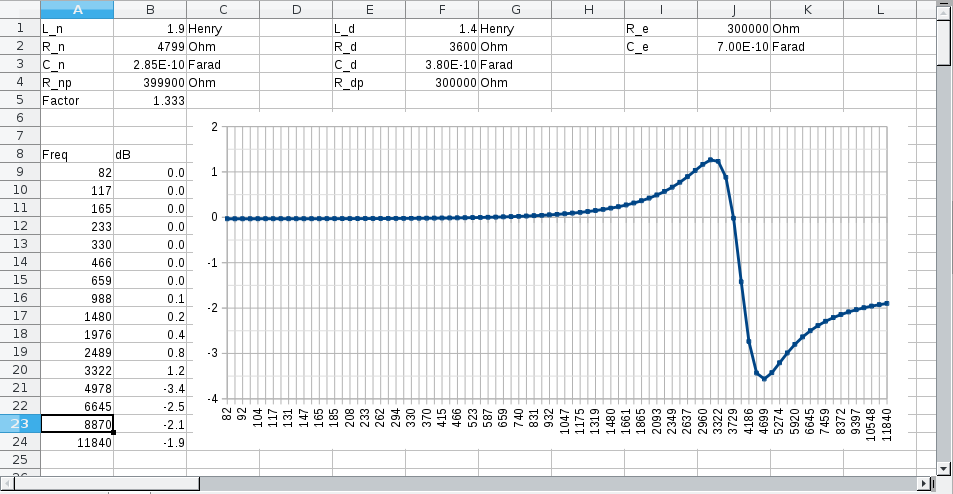 |
|
col
format tables
Posts: 474
Likes: 25
|
Post by col on Nov 25, 2017 19:38:45 GMT -5
By extension, are similar five-coil arrangements fully him-cancelling?
Coils: PU1 (A,B); PU2 (C,D); PU3 (E,F)
For example:
(AxCxE)+(BxD)
Or:
(A+C+E)x(D+F)
I was playing around with an idea and stumbled across this. The (im)practicality of trying to switch between various arrangements of five coils probably rules this out in reality. Particularly if we wish to avoid 'hanging from hot' and shunting.
|
|
|
|
Post by Yogi B on Nov 26, 2017 2:17:17 GMT -5
By extension, are similar five-coil arrangements fully hum-cancelling? Yes (albeit with the usual caveats concerning that "fully" hum-cancelling isn't really attainable). In fact out of the available 7552 series-parallel permutations of 5 coils, there are 930 possible permutations that would be fully hum-cancelling in idealised conditions. Or put another way 18 hum-cancelling combinations out of a possible 170 combinations. Those also include combinations with the same basic structure as those you suggest, but even more unbalanced: a single coil of "positive hum" offsetting 4 coils of "negative hum". Plus the fairly obvious combinations of a hum-cancelling 3-coil config and a hum-cancelling 2-coil config in global series or parallel with each other. However there are also others which currently make no intuitive sense to me, and only fall out when you run through the calculations of the the output. At one point I was going to start a thread containing all the hum-cancelling groupings for 2 to 6 coils, both as a reference and as a hope that someone could help to determine a pattern in which groupings are hum-cancelling, without resorting to manual calculations. Alas I've not got around to that, yet. |
|
|
|
Post by sumgai on Nov 26, 2017 10:53:37 GMT -5
In fact out of the available 7552 series-parallel permutations of 5 coils, there are 930 possible permutations that would be fully hum-cancelling in idealised conditions. Or put another way 18 hum-cancelling combinations out of a possible 170 combinations. Yogi, you have entirely too much time on your hands!  |
|
col
format tables
Posts: 474
Likes: 25
|
Post by col on Nov 26, 2017 18:59:30 GMT -5
By extension, are similar five-coil arrangements fully hum-cancelling? Yes (albeit with the usual caveats concerning that "fully" hum-cancelling isn't really attainable). Yeah. I understand that 'fully hum-cancelling' assumes matched pickups under ideal (in-theory) conditions. I'll work up my own figures here for that (since it is easy to miss sets, or unknowingly have them overlap). First, we would need to create an exhaustive list of basic patterns. I should say, I am generally only interested in creating 'fully' hum-cancelling options. That's quite a complication. And, I wish to strip out electrically identical patterns (so, a set of in-series permutations of one combination is counted just once - a 'combination'). This brings me onto another complication, regarding terminology. A set of five coils is a 'combination' (in the true sense of the term). For our purposes we are only interested in combinations (permutations of one combination being electrically identical to each other). However, these five coils can be arranged in a number of (electrically divergent) patterns (all in series and all in parallel being just two possibilities). So, I suggest using the terms: patterns; combinations; permutations. I'm going to test this (off the top of my head, that number seems to be very short). Key: x: series +: parallel (): inverted/reversed coil PU1: A,B PU2: C,D PU3: E,F Five coils from six = 6 combinations For a single 'pattern': Since any coil may be reversed, five coils may be split into any combination of 2 and 3. Any 2 coils from 5: 5!/3!/2! = 10 combinations Now, let's compared an all-in-phase arrangement with mismatched grouping of 2:3 from a set of 5 coils (where one or more coils must be inverted). (AxCxE)+(BxD) = (standard, all-in-phase orientation of coils) Ax(B)xE)+((C)xD) (2 inverted coils). Note, that is is one of the above 10 combinations! As far as I know, we cannot invert additional coils (in the above) and still have full hum-cancelling, and create a new electrically unique arrangement. If we instead invert 'D', we would have to invert 'A' and 'E' too - this would be electrically identical to previous version. So, we have 6 combinations of 5 coils. And in a 2:3 split coil arrangement (from any set of 5 coils), we have 10 combinations and available in 2 different (non-obvious) arrangements: (AxCxE)+(BxD) and (A+C+E)x(B+D). So, that 6x10x2 = 120 non-obvious, fully hum-cancelling 2:3 arrangements. Well, the 2:3 arrangement was not so obvious to me (read my earlier comments to this thread). But unless I'm mistaken, there are a whole lot more of those than you have suggested. I have not included the all-in-series or all-in-parallel arrangements, Nor have I included 4:1 arrangements. As I wrote earlier, I think the first thing to do is create an exhaustive list of (potentially) 'fully' hum-cancelling patterns. Well, you will have to describe them to me. There will be a large number of possible patterns with 4, 5 or 6 coils. I assume that hum-cancelling 3:1 arrangements are possible too. |
|
|
|
Post by Yogi B on Nov 27, 2017 2:55:16 GMT -5
Yogi, you have entirely too much time on your hands!  Well yes, but those numbers come from an underlying part of QCoils, so calculating them took less time than typing this sentence.
This brings me onto another complication, regarding terminology. A set of five coils is a 'combination' (in the true sense of the term). For our purposes we are only interested in combinations (permutations of one combination being electrically identical to each other). However, these five coils can be arranged in a number of (electrically divergent) patterns (all in series and all in parallel being just two possibilities). So, I suggest using the terms: patterns; combinations; permutations. I knew using permutations and combinations would land me in trouble! I was trying to avoid speaking in terms of graphs/networks, or using my own terminology. However, my trying to force words to have different meanings is probably more confusing. Firstly I'll point out that I'm only considering a total of 5 coils, rather than 5 out of 6 coils, as it makes the numbers more portable. If you have more pickups than the minimal requirement, you need only multiply the numbers by the relevant binomial coefficient in this case 6C 5 i.e. 6. As a side note, another thing I do different to aid generalisation is assume each coil is of the same magnetic and winding orientations, this makes no difference in terms of pure numbers, but it simplifies things as I don't have to label, then take into account that some coils are RWRP. Consider that in this thread that in the OP the magnetic polarities of A through D go S-N-S-N, whereas in a stock guitar we would more often be working with S-N-N-S. As such we would have to remember that either the pickup or the labels C and D are flipped, which is an extra mental step that I'd rather not have to perform. This issue only gets worse with HSH or HHH configurations. What I termed combinations in my last post, equate to your term patterns. Personally I've been using the word structures (which I should've stuck with), because it has adjective and adverb forms, allowing me to say things like "structurally equivalent". More technically this is the number of unique series-parallel networks with n unlabelled directed edges. Then by permutations I meant the unique ways of permuting the coils within those structures -- this is the number of unique series-parallel networks with n labelled directed edges. This is an example of where thinking of all the coils being the same orientation helps, because then this pattern can be written as (P x P x P) + (−P x −P), using − to denote reversed phase. Then we can easily see what we require for hum cancelling is a series group 3-coils producing "positive hum" in parallel with a series group 2-coils producing "negative hum". We can freely swap pickups in, out, and between the two series sub-groups and maintain hum cancellation, so long as they are (re-)orientated to observe this rule. In other words, your assumption of needing to invert the phase of both A and E, when inverting D, is incorrect. For example the arrangement (−D x −B x E) + (−C x −A) or more cleanly written when globally inverted as (B x D x −E) + (A x C) is also hum-cancelling. It's not only about creating that list though, it's also ordering and formatting it in a way such that it stands a chance of being comprehensible -- you probably don't want a 150+ line wall/column/tower of text. For now these are the two (involving 5 pickups) which are most confusing to me (note that they are each other's dual), along with visualisations of them as directed graphs. It's relatively simple to work out that the impedance and hum output of the 4-coil sub groups is equivalent to a single coil, and thus is cancelled by remaining coil. The issue I have with them is that the unlike the other 5-coil structures, they cannot be built from smaller hum-cancelling groups, either by inserting a single coil to a hum-cancelling 4-coil group or combining hum-cancelling 2-coil and 3-coil groups. ((P x P) + (P x −P)) x −P: 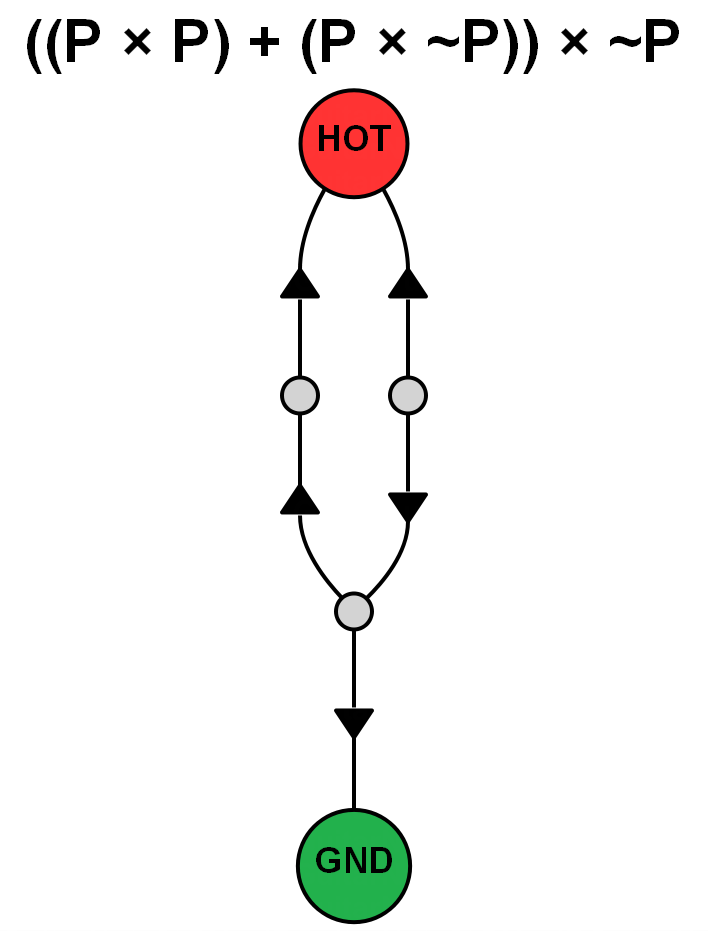
((P + P) x (P + −P)) + −P: 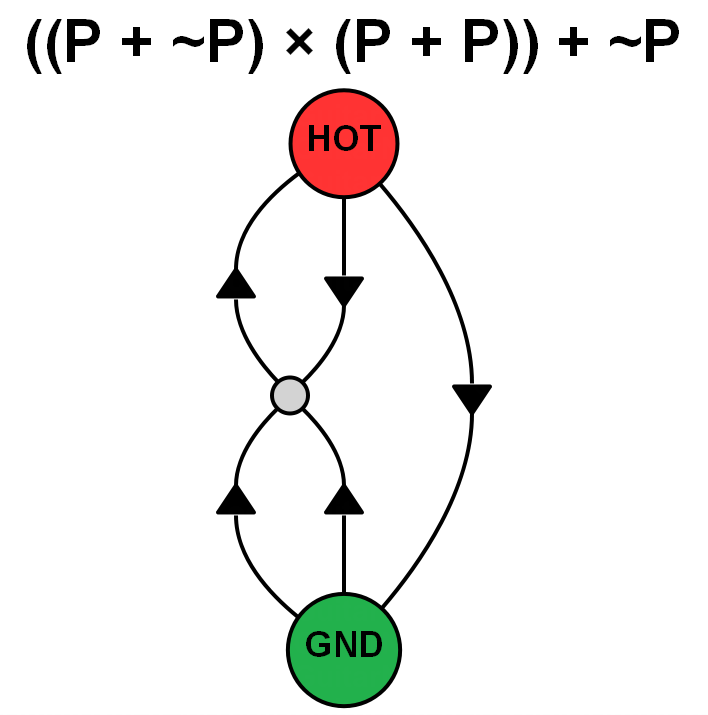
|
|
|
|
Post by JohnH on Nov 27, 2017 15:00:13 GMT -5
Nice puzzles!
I agree those two 5x combos above are nominally humcancelling. So I dont follow what is the issue with them?
|
|
col
format tables
Posts: 474
Likes: 25
|
Post by col on Nov 28, 2017 12:29:35 GMT -5
This brings me onto another complication, regarding terminology. A set of five coils is a 'combination' (in the true sense of the term). For our purposes we are only interested in combinations (permutations of one combination being electrically identical to each other). However, these five coils can be arranged in a number of (electrically divergent) patterns (all in series and all in parallel being just two possibilities). So, I suggest using the terms: patterns; combinations; permutations. I knew using permutations and combinations would land me in trouble! I was trying to avoid speaking in terms of graphs/networks, or using my own terminology. However, my trying to force words to have different meanings is probably more confusing. Firstly I'll point out that I'm only considering a total of 5 coils, rather than 5 out of 6 coils, as it makes the numbers more portable. If you have more pickups than the minimal requirement, you need only multiply the numbers by the relevant binomial coefficient in this case 6C 5 i.e. 6. As a side note, another thing I do different to aid generalisation is assume each coil is of the same magnetic and winding orientations, this makes no difference in terms of pure numbers, but it simplifies things as I don't have to label, then take into account that some coils are RWRP. Consider that in this thread that in the OP the magnetic polarities of A through D go S-N-S-N, whereas in a stock guitar we would more often be working with S-N-N-S. As such we would have to remember that either the pickup or the labels C and D are flipped, which is an extra mental step that I'd rather not have to perform. This issue only gets worse with HSH or HHH configurations. Ah. But I indicated using 5 from 6 coils in my original post, hence our cross purposes. Though, our numbers still do not match. For 2:3 types, in the two 'patterns' ('structures') I outlined, would result in 20 configurations ('combinations', if you like). Yes, your simplifications make sense, except if we need to consider OOP options separately. Some people are not interested in those sounds. OK, we can use 'structures'. OK. That might be confusing for some, but so long as things are defined within a post, that should work. For raw numbers, we can do as you suggest. Though, as I wrote before, it might be useful to differentiate between in-phase and OOP options. I'll give this some thought. I am probably quite good at doing this, but not so good at doing the calculations to check for 'full hum-cancelling'. guitarnuts2.proboards.com/post/62462 (be sure to view the last post (for missing images) for context). We are talking about 5 coils - exactly five coils - yes? The number of possible structures should not be too bad. What we could do is use the possible structures outlined by ChrisK (and the one I added) and add the fifth coil to each of those, in all differentiating locations. Probably not complicated. Well, I'll leave the math to you and others. I could work it out (the math was outlined earlier in this thread), but I'm sure you'd be faster. |
|
col
format tables
Posts: 474
Likes: 25
|
Post by col on Nov 28, 2017 18:29:05 GMT -5
This is my first run through this. I think there are 24 structures, but I'd need to double-check that (and if you, Yogi, and others too would check, I'd appreciate it).
I'm going to go through this as systematically as possible. Working from ChrisK's patterns is not that useful, as it is too easy to unwittingly create similar structures that way. I've gone for a different approach; going from a single tier, right through to 5 tiers.
Single Tier (5):
1
___________
.| | | | |
.O O O O O
_|_|_|_|_|_
2 Tiers (4:1):
2a...........2b...........2c...........2d
_________...._________...._________...._________
.| | | |......| | | |......| | | |......| | | |
.O O O O......O O O O......O O O O......O O O O
.|_|_|_|......|_|_| |......|_| | |......| | | |
.|............|.....|......|...| |......| | | |
.O............O.....|......O...| |......O | | |
_|_ _ _ _...._|_ _ _|_...._|_ _|_|_...._|_|_|_|_
2 Tiers (3:2):
2.1a.......2.1b.......2.1c.......2.1d
_______...._______...._______...._______
.| | |......| | |......| | |......| | |
.O O O......O O O......O O O......O O O
.|_|_|......| |_|......|_| |......| | |
.| |........| |........| | |......| | |
.O O........O O........O O |......O O |
_|_|_ _...._|_|_ _...._|_|_|_...._|_|_|_
3 Tiers (3:1:1):
3a.........3b.........3c.........3d.........3e.........3f
_______...._______...._______...._______...._______...._______
.| | |......| | |......| | |......| | |......| | |......| | |
.O O O......O O O......O O O......O O O......O O O......O O O
.|_|_|......|_| |......| | |......| | |......|_| |......| | |
.|..........|...|......| | |......| | |......|...|......| | |
.O..........O...|......O | |......O | |......O...|......O | |
.|..........|...|......|_| |......| | |......|_ _|......|_|_|
.|..........|...|......|...|......| | |......|..........|
.O..........O...|......O...|......O | |......O..........O
_|_ _ _...._|_ _|_...._|_ _|_...._|_|_|_...._|_ _ _...._|_ _ _
3 Tiers (2:2:1):
3.1a.....3.1b.....3.1c.....3.1d
_____...._____...._____...._____
.| |......| |......| |......| |
.O O......O O......O O......O O
.| |......|_|......| |......|_|
.| |......| |......| |......| |
.O O......O O......O O......O O
.|_|......|_|......| |......| |
.|........|........| |......| |
.O........O........O |......O |
_|_ _...._|_ _...._|_|_...._|_|_
4 Tiers (2:1:1:1):
4a.......4b.......4c.......4d
_____...._____...._____...._____
.| |......| |......| |......| |
.O O......O O......O O......O O
.|_|......| |......| |......| |
.|........| |......| |......| |
.O........O |......O |......O |
.|........|_|......| |......| |
.|........|........| |......| |
.O........O........O |......O |
.|........|........|_|......| |
.|........|........|........| |
.O........O........O........O |
_|_ _...._|_ _...._|_ _...._|_|_
5 Tiers (1:1:1:1:1):
5
___
.|
.O
.|
.|
.O
.|
.|
.O
.|
.|
.O
.|
.|
.O
_|_
Crap. That was a lot more time-consuming than I anticipated. I was going to use a code box because preview mode suggested that a code box would retain the extra blank spaces - nope. More than one space between 'words' is removed.
|
|
|
|
Post by Yogi B on Nov 29, 2017 0:47:05 GMT -5
I dont follow what is the issue with them? It's that I was fixated with the idea that the rules that enable one to generate the hum-cancelling 3-coil structures from the hum-cancelling 2-coil structures, and the 4-coil ones from both the 3-coil and 2-coil ones, should also work for the 5-coil ones. Yet these two cannot and rely on a new rule, but I need to think about it differently -- it isn't a new rule it's the same as gives the original hum-cancelling 2-coil structures.
Though, our numbers still do not match. For 2:3 types, in the two 'patterns' ('structures') I outlined, would result in 20 configurations ('combinations', if you like). And I would agree, and as far as I'm aware haven't suggested otherwise -- so what are you comparing 20 with? One thing I thing we still haven't explicitly covered (and seem to have different ideas on) is whether a structure is independent of phasing, in other words is a structure a directed or undirected network. This boils down to the question of whether P + P and P + -P are separate structures. My answer would be "yes", but I think that your answer is "no". Perhaps we need to differentiate between "phased structures" and "un-phased structures" -- I think this confusion stems from the fact that the in-phase-only phased-structures are essentially equivalent to the un-phased structures. Possibly, but it's not simple as it depends on the pickup coils being used. Looking at P + -P it illustrates that we need one coil of "positive hum" and one of "negative hum" in order to achieve hum cancelling. But how we get those may vary: - if for example we have two coils that share winding direction and magnetic polarity (e.g. A and C) then in order to get our "negative hum" we need to invert the phase of one coil (e.g. A + -C), resulting in an out-of-phase sound;
- however, if we have one 'normal' coil and one RWRP coil (e.g. A and B), since the RWRP coil already gives us "negative hum" it doesn't need to be inverted (i.e. A + B), resulting an in-phase sound.
So really all options can be produced as in-phase versions it just depends on the number of normal and RWRP coils we have available. As a further example consider (P x P x P) + -P, this cannot be achieved as an in-phase sound with typical HSS or HH configurations, but it is possible via careful selection of coils from HSH or HHH configurations.
Yep,  I'm sure that wasn't always the case, perhaps ProBoards introduced it as a way to free up room on their servers -- by not saving spaces, saving space! Edit: it's only a few months later... but I've been reminded that [pre] tags are a thing! |
|
col
format tables
Posts: 474
Likes: 25
|
Post by col on Nov 29, 2017 1:14:28 GMT -5
Hi Yogi,
I am about to log off. I'll try to reply tomorrow.
Just to say, I think we might be a little at cross-purposes. For the purposes of my diagrams, I decided that I would not be addressing polarity: 1) it is (as you suggested) easier to not address it; and 2) I have not run the math to see which structures are potentially hum-cancelling.
As for the '20 combinations' (10 each, from diagrams 2.1a and 3.1c in my last post) - you seemed to suggest in an earlier post that there are just 18 possible combinations from the two 2:3-type structures. Hmm. I'm going to have to edit those diagrams in my last post to add some extra labels.
Bye for now.
|
|
|
|
Post by Yogi B on Nov 30, 2017 2:11:43 GMT -5
18 is the number hum-cancelling 5-coil structures, when assigned the correct reversed-phase or RWRP coils 2.1a and 3.1c are 2 of those. As you point out, there are also ways of swapping coils around between the subgroups of those structures. In this case determined by the number of 2 (or 3) length combinations from 5 as we have a 3-coil sub-group and a 2-coil sub-group, this results in 10 ways to assign the positions of the coils from our chosen 5-coil combination, per each of those two structures -- resulting in your 20. (And that's only considering the un-phased versions of that structure). What I don't think we have a proper term for are these 10 differing results, I'm hesitant to say "combinations" here as we've already picked a true combination by selecting which of the total available coils we're using. I would say "sounds", but as mentioned above the with the perceivable difference being potentially small, "sounds" feels too inexact and subjective. The other alternatives, I could suggest are "arrangements" and "configurations", and although I'm going to use "arrangements" for the rest of this post, I welcome other suggestions. In short my 18 is referring to structures and your 20 is referring to arrangements.Here's a couple of examples, that hopefully further illustrate how I'm thinking: - Available coils: A B C
- Combination: A B C
- Un-phased structure: (P x P) + P
- Phased structure: (P x P) + P
- Arrangement: (A x C) + B
- Available coils: A B C
- Combination: A C
- Un-phased structure: P + P
- Phased structure: P + -P
- Arrangement: A + -C
There's also an additional terminological issue I've been meaning to bring up, that of describing a resulting sound or arrangement as being "in-phase" or "out-of-phase", what is it "in" or "out of" phase with? What we mean is: all of the coils within this arrangement are in-phase with each other; or, one or more pickups is out-of-phase with the others. This may be okay in general usage, and whilst it starts to get ambiguous with multiple in-phase items, it's when referring to a collection of things as being out-of-phase things can get confusing. A familiar example is the difference in meaning between "a neck humbucker out-of-phase with a bridge humbucker" and "a (neck) humbucker out-of-phase with itself". The terms that seems most obvious to use are "homo-phased" and "hetero-phased" with "pan-phased" for both/either, yet I've previously used "un-phased" and "sans-phase" when explicitly not considering phasing and I'd prefer to not mix Greek & Latin prefixes if I can help it. Maybe we should go with something plainer like "single-phase" and "mixed-phase" instead?
Anyway, now that we've hashed out some terminology, here's an attempt to better explain to what the numbers from that post were referring: Arrangements: Single-phase 5-coil arrangements: 472
Mixed-phase 5-coil arrangements: 7080
Total 5-coil arrangements: 7552
Assuming there are no RWRP coils then,
Hum-cancelling single-phase 5-coil arrangements: 0
Hum-cancelling mixed-phase 5-coil arrangements: 930
Total hum-cancelling 5-coil arrangements: 930 Structures: Single-phase 5-coil structures: 24
Mixed-phase 5-coil structures: 146
Total 5-coil structures: 170
Assuming there are no RWRP coils then,
Hum-cancelling single-phase 5-coil structures: 0
Hum-cancelling mixed-phase 5-coil structures: 18
Total hum-cancelling 5-coil structures: 18 Note that the distribution of the arrangements/structures which are hum-cancelling, between those that are single-phase and mixed-phase, is dependent on the ratio of 'normal' to RWRP coils. My assumption that there are no RWRP coils thus avoids arbitrarily splitting them between those two groups.
Hope that lot helps us think on the same page. |
|