3 pup coil hum-canceling

[newey]

a (neck) humbucker out-of-phase with itself"

As long as we're trying to be precise with our terminology, I think it is better to say "neck HB with its coils out of phase".

[Yogi B]

Dec 1, 2017 6:55:51 GMT -5 newey said:

I think it is better to say "neck HB with its coils out of phase".

To some degree I'm playing devil's advocate here, but is that really any better?

Out of context it is still not clear whether it is "one of its coils out of phase" (with respect to the  other), or if it is "both of its coils out of phase" (with some sort of global preordained in-phase direction). For instance at the point where that sentence ends, someone could easily continue "with the coils of the bridge HB".

[Yogi B]

Nov 27, 2017 2:55:16 GMT -5 Yogi B said:

For now these are the two (involving 5 pickups) which are most confusing to me (note that they are each other's dual), along with visualisations of them as directed graphs. It's relatively simple to work out that the impedance and hum output of the 4-coil sub groups is equivalent to a single coil, and thus is cancelled by remaining coil. The issue I have with them is that the unlike the other 5-coil structures, they cannot be built from smaller hum-cancelling groups, either by inserting a single coil to a hum-cancelling 4-coil group or combining hum-cancelling 2-coil and 3-coil groups.

((P x P) + (P x −P)) x −P	((P + P) x (P + −P)) + −P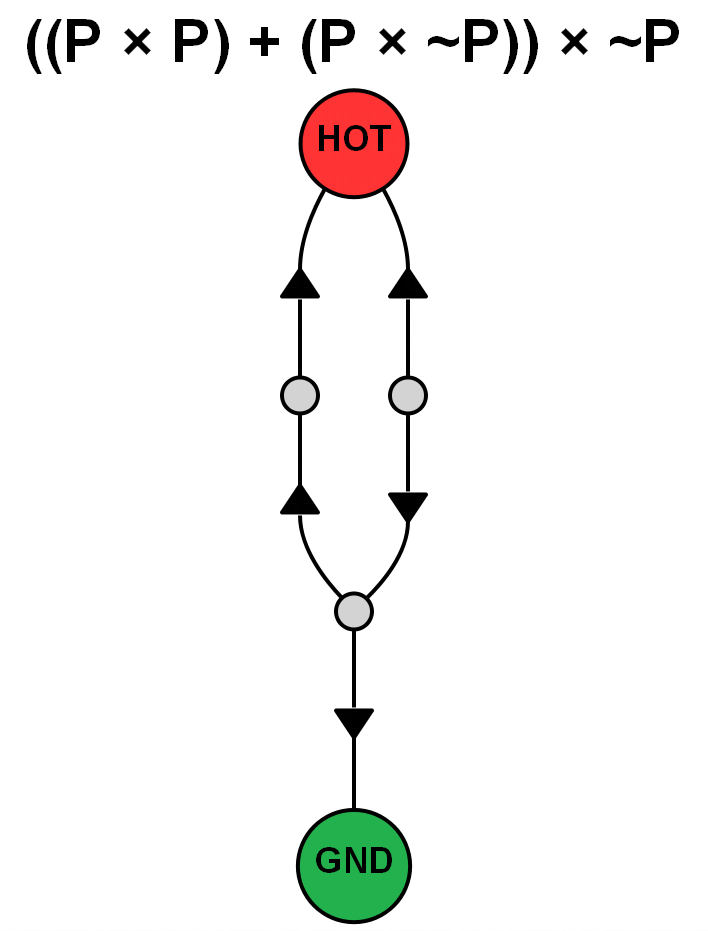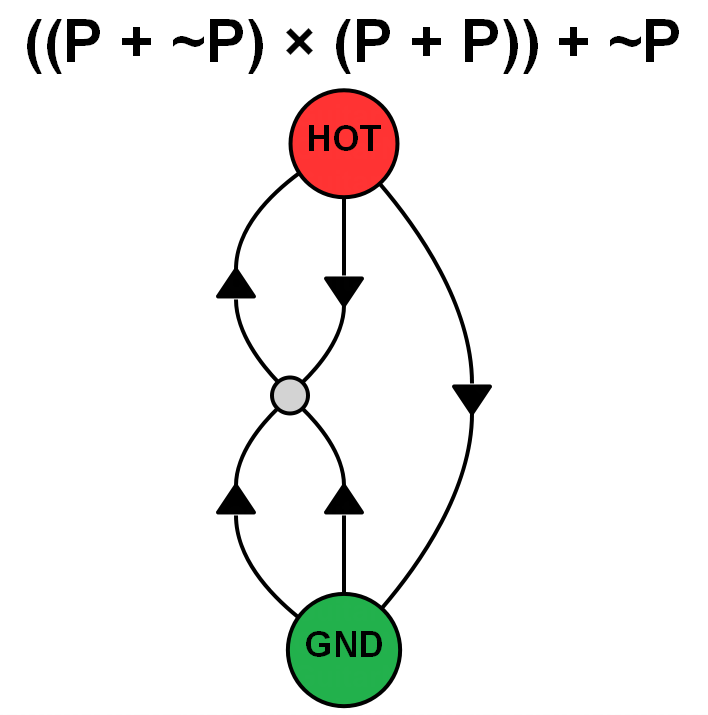

I took me a while, but I've spotted how these work. It's caused by the equivalence of (A × B) + (C × D) and (A + C) × (B + D) in certain circumstances, visually that is:

Essentially   Essentially
 Parallel       Series

   _|_           _|_
  |   |         |   |
 [A] [C]       [A] [C]
  |   |   ---   |___|
  |   |   ---   |   |
 [B] [D]       [B] [D]
  |_ _|         |_ _|
    |             |

The total voltage of the essentially parallel arrangement, V_P, and essentially series arrangement, V_S, are given by:\begin{cases}
V_P &\kern-1.4ex= \dfrac{(V_A + V_B) \cdot (Z_C + Z_D) + (V_C + V_D) \cdot (Z_A + Z_B)}{Z_A + Z_B + Z_C + Z_D}  \\[1.5em]
V_S &\kern-1.4ex= \dfrac{V_A \cdot Z_C + V_C \cdot Z_A}{Z_A + Z_C} + \dfrac{V_B \cdot Z_D + V_D \cdot Z_B}{Z_B + Z_D}
\end{cases}Where V_{(i)} and R_{(i)} represent the voltage output an impedance, respectively, of each pickup coil.

Thus, assuming idealised coils with identical impedances, Z_A = Z_B = Z_C = Z_D = Z, we can show that V_P = V_S:

SPOILER: Click to show

\begin{aligned}
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{(V_A + V_B) \cdot (Z + Z) + (V_C + V_D) \cdot (Z + Z)}{Z + Z + Z + Z}  \\\\
V_S &\kern-1.4ex= \dfrac{V_A \cdot Z + V_C \cdot Z}{Z + Z} + \dfrac{V_B \cdot Z + V_D \cdot Z}{Z + Z}
\end{cases}
\\\\
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{(V_A + V_B + V_C + V_D) \cdot \bcancel{2Z}}{{}^2\;\bcancel{4Z}}  \\\\
V_S &\kern-1.4ex= \dfrac{(V_A + V_C) \cdot \bcancel{Z}}{2\bcancel{Z}} + \dfrac{(V_B + V_D) \cdot \bcancel{Z}}{2\bcancel{Z}}
\end{cases}
\\\\
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{V_A + V_B + V_C + V_D}{2}  \\\\
V_S &\kern-1.4ex= \dfrac{V_A + V_C + V_B + V_D}{2}
\end{cases}
\end{aligned}

In fact, this is also true when Z_A = Z_C = Z_{AC} & Z_B = Z_D = Z_{BD}

SPOILER: Click to show

\begin{aligned}
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{(V_A + V_B) \cdot (Z_{AC} + Z_{BD}) + (V_C + V_D) \cdot (Z_{AC} + Z_{BD})}{Z_{AC} + Z_{BD} + Z_{AC} + Z_{BD}}  \\\\
V_S &\kern-1.4ex= \dfrac{V_A \cdot Z_{AC} + V_C \cdot Z_{AC}}{Z_{AC} + Z_{AC}} + \dfrac{V_B \cdot Z_{BD} + V_D \cdot Z_{BD}}{Z_{BD} + Z_{BD}}
\end{cases}
\\\\
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{(V_A + V_B + V_C + V_D) \cdot (Z_{AC} + Z_{BD})}{2 \cdot (Z_{AC} + Z_{BD})}  \\\\
V_S &\kern-1.4ex= \dfrac{(V_A + V_C) \cdot \bcancel{Z_{AC}}}{2 \cdot \bcancel{Z_{AC}}} + \dfrac{(V_B + V_D) \cdot \bcancel{Z_{BD}}}{2 \cdot \bcancel{Z_{BD}}}
\end{cases}
\\\\
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{V_A + V_B + V_C + V_D}{2}  \\\\
V_S &\kern-1.4ex= \dfrac{V_A + V_C + V_B + V_D}{2}
\end{cases}
\end{aligned}

And when Z_A = Z_B = Z_{AB} & Z_C = Z_D = Z_{CD}

SPOILER: Click to show

\begin{aligned}
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{(V_A + V_B) \cdot (Z_{CD} + Z_{CD}) + (V_C + V_D) \cdot (Z_{AB} + Z_{AB})}{Z_{AB} + Z_{AB} + Z_{CD} + Z_{CD}}  \\\\
V_S &\kern-1.4ex= \dfrac{V_A \cdot Z_{CD} + V_C \cdot Z_{AB}}{Z_{AB} + Z_{CD}} + \dfrac{V_B \cdot Z_{CD} + V_D \cdot Z_{AB}}{Z_{AB} + Z_{CD}}
\end{cases}
\\\\
&\begin{cases}
V_P &\kern-1.4ex= \dfrac{\bcancel{2} \cdot \big[ (V_A + V_B) \cdot Z_{CD} + (V_C + V_D) \cdot Z_{AB} \big]}{\bcancel{2} \cdot (Z_{AB} + Z_{CD})}  \\\\
V_S &\kern-1.4ex= \dfrac{(V_A + V_B) \cdot Z_{CD} + (V_C + V_D) \cdot Z_{AB}}{Z_{AB} + Z_{CD}}
\end{cases}
\end{aligned}

What does this mean in relation to the two five-coil cases quoted above, lets examine the essentially parallel structure, ((P + P) × (P + -P)) + -P, we now know that under idealised conditions this is equivalent to ((P × P) + (P × -P)) + -P which is simply a parallel combination of the two hum-cancelling structures (P × -P) and (P × P) + -P.

Likewise the essentially series version, ((P × P) + (P × -P)) × -P is equal to (P + P) × (P + -P) × -P which is a series combination of the two hum-cancelling structures (P + -P) and (P + P) × -P.

[col]

Yogi B I don't believe I've read your post, above, before. I am bumping this now because I wish to clarify how your proposition that 'essentially parallel = essentially series' relates to this thread:

guitarnuts2.proboards.com/thread/3239/coil-combinations

I would be more than happy to learn after all these years that I (and those here who reluctantly ended up agreeing with me) were actually wrong, and that the late, great ChrisK was correct all along.

[col]

In case you missed the above, Yogi B, a bump.

[newey]

I think all of the discussion in ChrisK's thread, and in YogiB's above, is summarized (by Yogi) thusly:

Jul 29, 2019 12:05:29 GMT -5 Yogi B said:

assuming idealised coils with identical impedances

If we make that assumption, then the maths indicate there is no difference betweeen the parallel pairs in series or the series pairs in parallel. But real world, coils aren't identical, so we more-or-less concluded that ChrisK had omitted (either inadvertently or perhaps intentionally) the 4 combinations that you, col, identified. I don't think Yogi B is saying anything different.

Of course, real world, coils aren't identical, but it occurs to me it would be easy to test the proposition if one had a HH (with identical HBs)guitar wired such that each HB had a series/parallel switch, plus a global series/parallel switch inter-pickups. Someone around here must have a guitar with that arrangement. We could at least then note if there is a noticable tonal difference.

[col]

Hi newey,

I am looking at this more from the perspective of: if we accept that the coils are not only nominally identical, but are actually identical, would the two different arrangements result in two different tones simply because of the disparate sources (each coils sensing different sections of the string)?

Although there was pretty broad consensus, I am not sure we ever fully resolved the question.

[Yogi B]

Jul 5, 2021 6:44:45 GMT -5 newey said:

Jul 29, 2019 12:05:29 GMT -5 Yogi B said:

assuming idealised coils with identical impedances

If we make that assumption, then the maths indicate there is no difference between the parallel pairs in series or the series pairs in parallel. But real world, coils aren't identical, so we more-or-less concluded that ChrisK had omitted (either inadvertently or perhaps intentionally) the 4 combinations that you, col, identified. I don't think Yogi B is saying anything different.

Kind of, although the two arrangements are still fundamentally different, and are only exactly equivalent under certain idealised circumstances, I believe that the variation in real-world coils that themselves are supposed to be identical isn't enough that I'd expect a perceivable difference.

My above post extends this to two pairs which are dissimilar to each other (e.g. a high-output humbucker & a low-output humbucker, or a humbucker & two AlNiCo single coils). The only configuration that could result in a significant difference between the configurations is when we have a single odd one out of the four. But even then it's not as though the electrical properties of typical guitar pickups vary by orders of magnitude — so in the case of one odd coil, though I'd expect some difference, I would not expect that difference to be huge.

Of course, real world, coils aren't identical, but it occurs to me it would be easy to test the proposition if one had a HH (with identical HBs) guitar wired such that each HB had a series/parallel switch, plus a global series/parallel switch inter-pickups. Someone around here must have a guitar with that arrangement.

(Or even non-identical HBs, see above.) Some Jimmy Page style wirings do this, and I did have a guitar that could, but it's currently sitting as an empty shell with no electronics. I never did any explicit A/B testing, either with the guitar itself (as toggling between the two modes required 5 switches) or with recordings, but from what I remember there was little (if any) difference.

Jul 5, 2021 7:08:51 GMT -5 col said:

I looking this more from the perspective of: if we accept that the coils are not only nominally identical, but are actually identical, would the two different arrangements result in two different tones simply because of the disparate sources (each coils sensing different sections of the string)?

Pickup placement, in terms of the section of string that is sensed, should make no difference. In the equations from my above post I've deliberately only equated certain pairs of coil impedances, whereas I've left all four coil voltages independently variable.

However something that I'm not taking into account, which is influenced by placement, is if any of the coils share significant mutual inductances. This could potentially produce differing results, even with otherwise perfectly identical coils.

[col]

Hi Yogi B,

Thanks for the reply.

So, it seems, we are pretty-much where we were before in our understanding of this matter. That is to say, there are likely to be some appreciative differences in the real world, even with idealised (identical) pickups. But, as things stand, these differences cannot be quantified without some proper experimentation and analysis. Is that about right?

I suppose all we can do now is guess if ChrisK's omission was an oversight or by design.

[col]

Apr 9, 2016 20:30:17 GMT -5 JohnH said:

Col - yes there really are fully humcancelling combos of three coils, assumed similar except for polarity.

eg, for a combo sounding in phase, First, put two south coils in series. That creates a combined result with twice the hum, but also twice the impedance. Put that group in parallel with one north coil, which has -1 x hum and 1x impedance. The net result is zero hum because of the combination of hum from the two south coils, but with greater impedance, balances the lesser hum, with lesser impedance fro the north. The analysis of that is very similar to our discussion of the sound of these hybrid combos, see the current 'does this make a difference?' thread.

What happens is that, due to voltage divider action of the three coil impedances, the output sees 1/3 of the hum generated by each of the two series south coils, which is balanced by 2/3 of the anti-hum from the north coil, to make full hum cancellation.

I know all this is true because two of my guitars do this. In fact it was the surprise of first noticing this effect that got me interested again in guitar electronics about 10 years ago.

I cannot locate this thread. Anyone?

[Yogi B]

col, probably this one: Does this make any difference?

[col]

Jul 6, 2021 17:26:35 GMT -5 Yogi B said:

col, probably this one: Does this make any difference?

Ah. I tried a thread title search, but a typo in the original comment ('a' vs 'any' difference) derailed it. Thanks, Yogi B.

[col]

And I now see/realise that I had posted to that thread. Forgot all about it.

[col]

I was actually looking for something else when I came across this patent:

patents.google.com/patent/US10380986B2/en

It is complicated (and very long). I cannot quite get my head around the basic premise. But, I note, it mentions easy methods for calculating 'all humbucking combinations', and I thought this might be useful to (some of) this discussion.

[Yogi B]

Jul 27, 2021 9:34:40 GMT -5 col said:

I was actually looking for something else when I came across this patent: patents.google.com/patent/US10380986B2/en

It is complicated (and very long). I cannot quite get my head around the basic premise. But, I note, it mentions easy methods for calculating 'all humbucking combinations', and I thought this might be useful to (some of) this discussion.

It cites another patent by the same author which is more focused on the math: patents.google.com/patent/US10217450B2/en

(By the way, it's a much easier read when viewed as a pdf, which can be found in the heading.)

Which delightfully includes:

This invention makes the point that all possible and potentially useful two-terminal sensor or pickup circuits can be determined, so that switching systems can be designed that don't produce either a lot of duplicated tones, or tones that are non-humbucking, and thus noisy. This invention develops the math, phases and topologies necessary to determine just how many unique tones one may get from the numbers of pickups that can reasonably fit on or in a stringed instrument, particularly guitars. This increases the number of possible tones up to orders of magnitude over current choices using 3-way and 5-way electromechanical switches.
...
This patent application claims all topologies and tonalities developed for any number sensors of number J from 1 to infinity, constructed by the methods shown here, except for those already in the public domain and/or protected by patent.

To which I wish to know: which series-parallel "topologies" are considered public domain? Two, three, four, five, six pickups in series? Fine you can have those -- but 24,389 pickups in series? Nope, that's my novel invention!

The online encyclopaedia of integer sequences literally has a page for the sequence which counts all such topologies: oeis.org/A006351 (and has had since 1991-07-11).

Whereas "phases" are counted by: oeis.org/A005172 (added on 1991-05-16).

The promised calculations for "all humbucking combinations", would be new (to me at least), but based on the below, I'm not filled with much optimism.

Plus I've previously Googled the 'correct' number of hum-cancelling combinations for 6 & 7 coils (13,642 & 269,556 respectively) looking to corroborate those numbers and didn't land on this patent.

---

So far I've read up to "Math 3b" of this second patent, in which I've discovered an error. The correct number of distinct topologies (series-parallel networks with all pickups in phase) for four pickups is 52 (as noted in the OEIS sequence linked above), not the 58 as claimed by the patent.

The error is that the patent's maths double-counts some combinations, specifically it counts:

1. (A+B)×(C+D) and (C+D)×(A+B)
2. (A+C)×(B+D) and (B+D)×(A+C)
3. (A+D)×(B+C) and (B+C)×(A+D)

as 6 separate topologies, rather than correctly as 3. Likewise for (A×B)+(C×D) and similar, thus the total overcount by six.

To be expected, the overcounting gets worse as the number of pickups increases:

	Number of coils
	1	2	3	4	5	6
OEIS A006351 (correct)	1	2	8	56	472	5504
Patent US10217450B2	1	2	8	58	502	7219

[col]

Hi Yogi,

I thought you might be interested in this and would be able to decipher patent's contents. I spotted the linked patent later on in my skimming, but figured anyone interested enough to read the patent would find it.

As for:

This patent application claims all topologies and tonalities developed for any number sensors of number J from 1 to infinity, constructed by the methods shown here, except for those already in the public domain and/or protected by patent.

That's quite the carve out claimed there. But, of course, even if enforceable - and I am not sure it is - this does not prevent 'pickup topologies' created by any other means. I have quite the loathing for these kinds of patents (discoveries). Claiming patents for genes which exist in nature is a prime example of patent abuse. I also wonder what effect his error in the patent application would have on the enforceability?

PS Edited to add: I thought I'd look up patenting of genes, because I could not recall the state of play. A court ruling in the US (where these problems existed) deemed that genes are not patentable back in 2013. However, there have been attempts to create new law to allow such patents. Patently (please forgive the pun) a very bad idea.

www.sciencemag.org/news/2019/06/controversial-us-bill-would-lift-supreme-court-ban-patenting-human-genes

PPS As for patents of formulae: seems to be a grey area. It appears that the formulae themselves are not patentable, but applications of the formulae into tangible products may be:

What Are Abstract Ideas?

Abstract ideas are concepts like pure mathematics and algorithms. You cannot patent a formula. However, you can patent an application of that formula. Thus, while you cannot patent a mathematical formula that produces nonrepeating patterns, you can patent paper products that use that formula to prevent rolls of paper from sticking together.

www.legalmatch.com/law-library/article/what-cant-be-patented.html

[newey]

The patent, if granted, would not be enforceable, for any number of reasons. Yogi B and col cite to several of the problems. You can't patent mathematics, and while a formula might theoretically be patentable (chemical formulas are, if you develop a new molecule, for example), I doubt what he is doing here would be so unique as to be patentable.What he is doing is essentially a trivial application of existing math concepts.

Also, patent "claims" have to be specific. The word "claim" is a term of art within patent law, one that has a particular meaning in the context of a patent application. Thus, wording such as "claims all topologies and tonalities developed for any number sensors of number J from 1 to infinity, constructed by the methods shown here, except for those already in the public domain and/or protected by patent." is nowhere near specific enough to be a "claim". Claiming (essentially) anything that has not been patented before or which is in the public domain isn't a "claim" of anything- the claim has to be an affirmative one: "I claim this specific thing is new and hasn't been done before". He's trying to say "I claim anything which I can claim and which hasn't already been claimed by someone else."

Drawing up the "claims" portion of a patent application is the most fraught part of the process, the one on which attorneys spend the most time. This "claim" wouldn't cut any ice in a courtroom.

[JohnH]

I hereby claim that 1+1=2, also that 1-1=0

By implication i claim that 2-2=0

Hence that 1+1-2=0

I therefore reserve the rights to all works derived from the above in engineering, science and other related work of mankind. Which is pretty much everything, with the possible exception of sliced bread (and therefore peanut butter and jelly sandwiches, which were never really that great anyways).

[col]

I keep re-reading this claim:

This patent application claims all topologies and tonalities developed for any number sensors of number J from 1 to infinity, constructed by the methods shown here, except for those already in the public domain and/or protected by patent.

...and I cannot quite work out its meaning. Is the Inventor claiming all 'topologies' he has 'discovered' via his 'method' (an infinite number of them - all possible (nominally) fully hum-cancelling combinations)? Or is he merely claiming all topologies which might be describe and developed using his formula? (That is to say, he is not claiming topologies which might be described (by others) with the proviso that they not developed using his method). I don't imagine it matters that much in the end, since the claim is probably indefensible either way. I just find it curious that it is ambiguous and my understanding that patents claims are expected to be rigorous and exacting (even more so that other legal documents).

And, I am not sure his method describes the two 5-coil configurations described in an earlier post by Yogi B. Hard to say for sure, because the document is difficult to penetrate.

guitarnuts2.proboards.com/thread/7639/3-pup-coil-hum-canceling?page=1&scrollTo=82746

[Yogi B]

Jul 27, 2021 9:34:40 GMT -5 col said:

But, I note, it mentions easy methods for calculating 'all humbucking combinations', and I thought this might be useful to (some of) this discussion.

Having read both patents further, and I think we're overexcitedly misreading "all humbucking combinations". The author's intention is more along the lines of "some number of combinations, all of which are humbucking", rather than "all possible humbucking combinations".

Jul 28, 2021 4:48:39 GMT -5 col said:

And, I am not sure his method describes the two 5-coil configurations described in an earlier post by Yogi B.

I'm pretty sure that it does not.

The section on humbucking combinations first creates topologies with 2n coils ("humbucking pairs, quads, hexes and octets"), by simply replacing each coil of an n-coil topology with a humbucking pair (either series or parallel). Humbucking arrangements of three coils are acknowledged as a "special case" which is then somewhat generalised to similar arrangements (e.g. (N×N×N)+S, (N+N+N)×(S+S), etc.), but this isn't fully expanded upon. For instance the author does not explore topologies containing both "humbucking triples" and "humbucking pairs". As such, the predicted numbers of humbucking combinations is vastly undercounted (though this is somewhat compensated by the previous overcounting).

[col]

Jul 28, 2021 5:43:12 GMT -5 Yogi B said:

Jul 27, 2021 9:34:40 GMT -5 col said:

But, I note, it mentions easy methods for calculating 'all humbucking combinations', and I thought this might be useful to (some of) this discussion.

Having read both patents further, and I think we're overexcitedly misreading "all humbucking combinations". The author's intention is more along the lines of "some number of combinations, all of which are humbucking", rather than "all possible humbucking combinations".

I am not sure about that. I gained the impression that his method is an attempt to describe all possible humbucking combinations up to infinity # of 'sensors'. But I expect that you have read the patent more carefully than me; and, more pertinently, understood it better too.

Jul 28, 2021 4:48:39 GMT -5 col said:

And, I am not sure his method describes the two 5-coil configurations described in an earlier post by Yogi B.

I'm pretty sure that it does not.

The section on humbucking combinations first creates topologies with 2n coils ("humbucking pairs, quads, hexes and octets"), by simply replacing each coil of an n-coil topology with a humbucking pair (either series or parallel). Humbucking arrangements of three coils are acknowledged as a "special case" which is then somewhat generalised to similar arrangements (e.g. (N×N×N)+S, (N+N+N)×(S+S), etc.), but this isn't fully expanded upon. For instance the author does not explore topologies containing both "humbucking triples" and "humbucking pairs". As such, the predicted numbers of humbucking combinations is vastly undercounted (though this is somewhat compensated by the previous overcounting).

Is it just me, or the nature of patents, or is that patent really confusing. I've looked at a few and found them generally understandable.

[newey]

Jul 28, 2021 8:36:12 GMT -5 col said:

is that patent really confusing

Yes. And, that's part of the reason it wouldn't stand up in a Courtroom. Keep in mind that having a patent doesn't actually get you anything except a right to sue someone for violating it. The process of filing for a patent is simply "notice to the world" that you are claiming a patent right. Your patent is only "valid" if, and when, a court says it is. And you still have to sue subsequent violators to enforce your patent rights (although subsequent lawsuits will be easier after a court has held the patent to be valid).

[col]

Jul 28, 2021 9:59:46 GMT -5 newey said:

Jul 28, 2021 8:36:12 GMT -5 col said:

is that patent really confusing

Yes. And, that's part of the reason it wouldn't stand up in a Courtroom. Keep in mind that having a patent doesn't actually get you anything except a right to sue someone for violating it. The process of filing for a patent is simply "notice to the world" that you are claiming a patent right. Your patent is only "valid" if, and when, a court says it is. And you still have to sue subsequent violators to enforce your patent rights (although subsequent lawsuits will be easier after a court has held the patent to be valid).

I've had this argument elsewhere in another (totally unrelated) field where the patent-holder asserted that because a patent had been granted, that this meant something more than she had fulfilled the most basic bureaucratic requirements to register the patent. She seemed to think that registration of the patent meant that it was enforceable. The patent application was - if you can believe it - much worse than the one we have discussed here. If you are remotely interested, newey, send me a PM and I'll provide a couple of links to you (I won't post details here to protect my privacy). The (US) patent system must be in a sorry state to have accepted the application.

Anyway - apologies for derailing another thread.

[unreg]

Jul 27, 2021 17:31:17 GMT -5 JohnH said:

Which is pretty much everything, with the possible exception of sliced bread (and therefore peanut butter and jelly sandwiches, which were never really that great anyways).

What about celery, cinnamon, and carrot sandwiches? Obviously they are made with sliced bread too…

2^0 + 1^0 = 2 (Do your original claims imply simplification? Or, can I use this? 😋).


EDIT: Oh, my above work is not derived from your post; rather, I was using knowledge gained from school.

[JohnH]

Jul 28, 2021 14:58:46 GMT -5 unreg said:

Jul 27, 2021 17:31:17 GMT -5 JohnH said:

Which is pretty much everything, with the possible exception of sliced bread (and therefore peanut butter and jelly sandwiches, which were never really that great anyways).

What about celery, cinnamon, and carrot sandwiches? Obviously they are made with sliced bread too…

2^0 + 1^0 = 2 (Do your original claims imply simplification? Or, can I use this? 😋).


EDIT: Oh, my above work is not derived from your post; rather, I was using knowledge gained from school.

No problem. I am ready to discuss licensing terms based on my prior sandwich.