Post by Yogi B on Jan 8, 2022 5:00:59 GMT -5
This has likely been done before, but my googling turned up nothing simple enough that I deemed it relevant to the world of stompboxes, and in any event I thought it was an interesting enough curiosity that it was worth sharing.
Recently I've been playing around with a few pedal ideas — one of which has only a moderate amount of additional volume (~4 dB) & pretty high output impedance, and therefore would benefit from the addition of a buffer and/or clean boost at the output.
Though there are a number of existing 'clean boost' pedals that do this kinda thing with an opamp (e.g. two distinct variations sail under MXR's colours: the Micro Amp and the MXR/CAE Boost / Line Driver) and while most have perfectly acceptable gain controls, I couldn't help but think that a better design may be possible.
What do I mean by "better"? Well the clue is in the thread title: I mean as close as possible to a linear relationship between the rotation of the gain potentiometer and the circuit's actual gain when measured in decibels. That is, ideally, if say a pedal has a maximum gain of 20 dB, then with the gain control set at noon (midway) it should give 10 dB of amplification, and at 9 o'clock (20%) it should boost by 4 dB, etc.
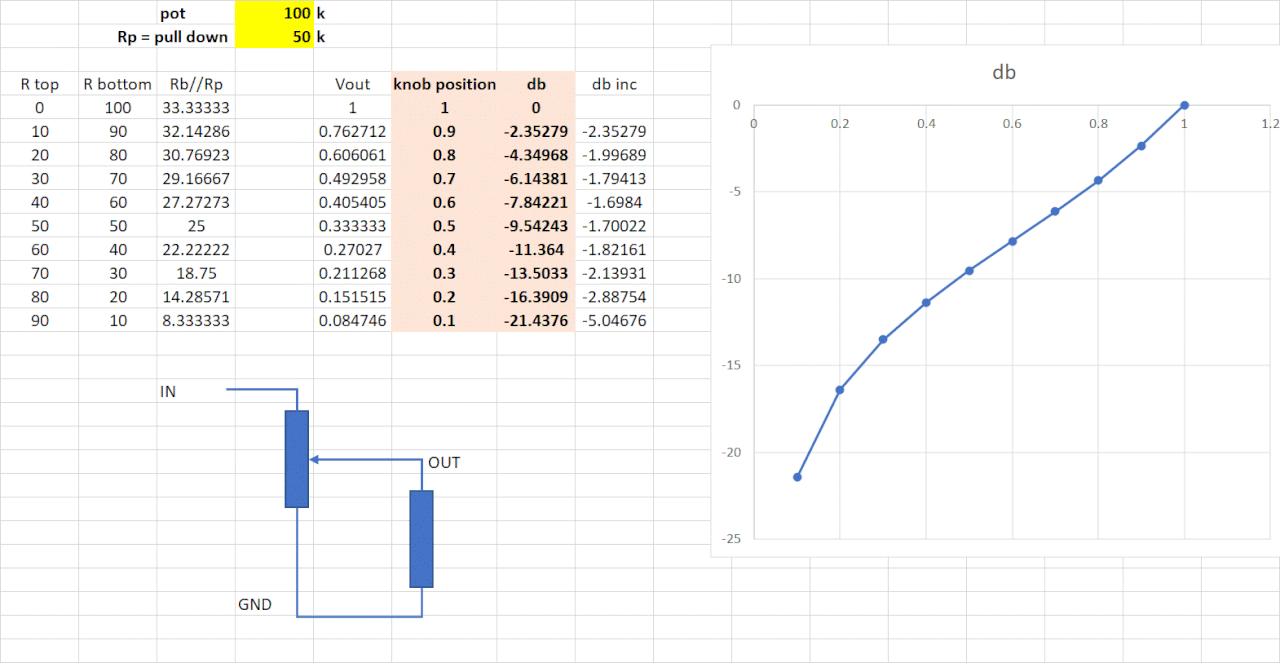
For the schematics I've looked at, some designs either appear to not care about giving a particularly linear response or were designed with other objectives in mind. The Micro Amp is one of these: the gain available ranges from approx. 500 mdB up to 26 dB — however, with the gain control set to noon the pedal gives 6 dB. And, although perhaps a reasonable design goal, is far from the 13.25 dB that would be required of a linear midpoint. Below is a graph showing the full response of the control, plotted in red — the horizontal axis is the fractional clockwise rotation of the pot, the vertical axis is gain measured in decibels. A straight line covering the same gain range is also present in purple (this isn't that useful here, with something quite obviously non-linear, but should prove useful in following graphs).

The other aforementioned pedal (MXR MC-401, Custom Audio Electronics: Boost / Line Driver), does quite a bit better at approximating a linear response:

At one time there was enough confidence in this (near) linearity that an early promo shot of the pedal features markings for +2 dB, +4 dB, +8 dB, +12 dB, +16 dB, and +20 dB — yet the production version only includes 0 dB, +10 dB and +20 dB. I suspect this change is, in part, a consequence of an inherent design 'problem' common to pedals of this type: their use of non-linear pots — the Line Driver uses an A100k and the Micro Amp uses a C500k.
So, while the above plot looks quite smooth and fairly accurate, it was produced using an idealised log taper. Whereas, if we were to use a piecewise linear approximation, more realistic to actual potentiometers, the result is less impressive:

Contrastingly, a linear taper potentiometer doesn't fall foul of this limitation of manufacturing (as it requires just one, constant, resistance gradient) and therefore doesn't fundamentally suffer from imprecision before even considering tolerances. Another possible advantage of utilising a linear taper is that it potentially opens up a wider choice of applicable pots, for example: if there was a need for an internal preset gain adjustment, most (if not all) trimmers are linear.
In the 'standard' circuits, usually only two terminals of the (log or anti-log) pot are used — a variable resistance inserted into either the negative feedback loop or between the inverting input and (virtual) ground. If using a linear taper, a different arrangement is required — below is what I came up with:

For a given maximum multiplicative gain, G > 1, (i.e. not decibels, G = 1 being equivalent to 0 dB) in order to get
As a neat (rational number) example, for G = 4 (a maximum gain of 12 dB), R1/Rp = 0.5, and R1/Rp = 1. Thus, if used with a 100 kΩ pot: R1 = 50 kΩ, R2 = 100 kΩ.
With less nice numbers, upping the maximum gain to 8 (18 dB), again with a 100 kΩ pot, yields R1 ≈ 21.1 kΩ and R2 ≈ 44.5 kΩ — this is the response I've chosen to plot below:

As you can see, the given response has a touch of an inverse-s-curve about it and unfortunately this gets worse as the gain range is increased. As such, the value of 18 dB (as used in the above plot) is roughly the maximum where I'd call the linearity of the response acceptable (it remains within 1 dB of the ideal response). The following graphs the dB difference from truly linear, for various values of G: 2√2, 4, 4√2, 8, 8√2, 16 (i.e. 9 dB, 12 dB, 15 dB, 18 dB, 21 dB, 24 dB, respectively), as usual for me, the plots are in spectral order (9 dB, G = 2√2, being red):

I'm curious whether this is something that others have bothered worrying about, or if anyone knows examples of clever circuits used to achieve the same goal.
Recently I've been playing around with a few pedal ideas — one of which has only a moderate amount of additional volume (~4 dB) & pretty high output impedance, and therefore would benefit from the addition of a buffer and/or clean boost at the output.
Though there are a number of existing 'clean boost' pedals that do this kinda thing with an opamp (e.g. two distinct variations sail under MXR's colours: the Micro Amp and the MXR/CAE Boost / Line Driver) and while most have perfectly acceptable gain controls, I couldn't help but think that a better design may be possible.
What do I mean by "better"? Well the clue is in the thread title: I mean as close as possible to a linear relationship between the rotation of the gain potentiometer and the circuit's actual gain when measured in decibels. That is, ideally, if say a pedal has a maximum gain of 20 dB, then with the gain control set at noon (midway) it should give 10 dB of amplification, and at 9 o'clock (20%) it should boost by 4 dB, etc.
For the schematics I've looked at, some designs either appear to not care about giving a particularly linear response or were designed with other objectives in mind. The Micro Amp is one of these: the gain available ranges from approx. 500 mdB up to 26 dB — however, with the gain control set to noon the pedal gives 6 dB. And, although perhaps a reasonable design goal, is far from the 13.25 dB that would be required of a linear midpoint. Below is a graph showing the full response of the control, plotted in red — the horizontal axis is the fractional clockwise rotation of the pot, the vertical axis is gain measured in decibels. A straight line covering the same gain range is also present in purple (this isn't that useful here, with something quite obviously non-linear, but should prove useful in following graphs).

The other aforementioned pedal (MXR MC-401, Custom Audio Electronics: Boost / Line Driver), does quite a bit better at approximating a linear response:

At one time there was enough confidence in this (near) linearity that an early promo shot of the pedal features markings for +2 dB, +4 dB, +8 dB, +12 dB, +16 dB, and +20 dB — yet the production version only includes 0 dB, +10 dB and +20 dB. I suspect this change is, in part, a consequence of an inherent design 'problem' common to pedals of this type: their use of non-linear pots — the Line Driver uses an A100k and the Micro Amp uses a C500k.
So, while the above plot looks quite smooth and fairly accurate, it was produced using an idealised log taper. Whereas, if we were to use a piecewise linear approximation, more realistic to actual potentiometers, the result is less impressive:

Contrastingly, a linear taper potentiometer doesn't fall foul of this limitation of manufacturing (as it requires just one, constant, resistance gradient) and therefore doesn't fundamentally suffer from imprecision before even considering tolerances. Another possible advantage of utilising a linear taper is that it potentially opens up a wider choice of applicable pots, for example: if there was a need for an internal preset gain adjustment, most (if not all) trimmers are linear.
In the 'standard' circuits, usually only two terminals of the (log or anti-log) pot are used — a variable resistance inserted into either the negative feedback loop or between the inverting input and (virtual) ground. If using a linear taper, a different arrangement is required — below is what I came up with:

For a given maximum multiplicative gain, G > 1, (i.e. not decibels, G = 1 being equivalent to 0 dB) in order to get
\sqrt{G} (half the maximum dB gain) at the mid-point of the pots rotation, the ratios of both R1 and R2 relative to the value of the pot, Rp, can be calculated via:
\begin{aligned}
{R_1 \over R_p} &= {1 - G + \sqrt{G^2 + 6G + 16\sqrt{G} + 9} \over 4(G - 1)}
\\[1.5em]
{R_2 \over R_p} &= {3 + 4\sqrt{G} + G + \sqrt{G^2 + 6G + 16\sqrt{G} + 9} \over 4\sqrt{G}(G - 1)}
\end{aligned}
As a neat (rational number) example, for G = 4 (a maximum gain of 12 dB), R1/Rp = 0.5, and R1/Rp = 1. Thus, if used with a 100 kΩ pot: R1 = 50 kΩ, R2 = 100 kΩ.
With less nice numbers, upping the maximum gain to 8 (18 dB), again with a 100 kΩ pot, yields R1 ≈ 21.1 kΩ and R2 ≈ 44.5 kΩ — this is the response I've chosen to plot below:

As you can see, the given response has a touch of an inverse-s-curve about it and unfortunately this gets worse as the gain range is increased. As such, the value of 18 dB (as used in the above plot) is roughly the maximum where I'd call the linearity of the response acceptable (it remains within 1 dB of the ideal response). The following graphs the dB difference from truly linear, for various values of G: 2√2, 4, 4√2, 8, 8√2, 16 (i.e. 9 dB, 12 dB, 15 dB, 18 dB, 21 dB, 24 dB, respectively), as usual for me, the plots are in spectral order (9 dB, G = 2√2, being red):

I'm curious whether this is something that others have bothered worrying about, or if anyone knows examples of clever circuits used to achieve the same goal.