Measuring the magnetic flux in the string.

[ms]

The plot shows the axial magnetic flux density in a plain G string from a 10s set of NYXL strings in one direction measured along the string from the center of the magnet that magnetizes the string. This is similar to a measurement Zollner performs. His relevant chapter section from Physics of the Electric Guitar is viewed here (I have not looked in his new book yet to see if he has more.):

relevant subsection of Zollner's first book



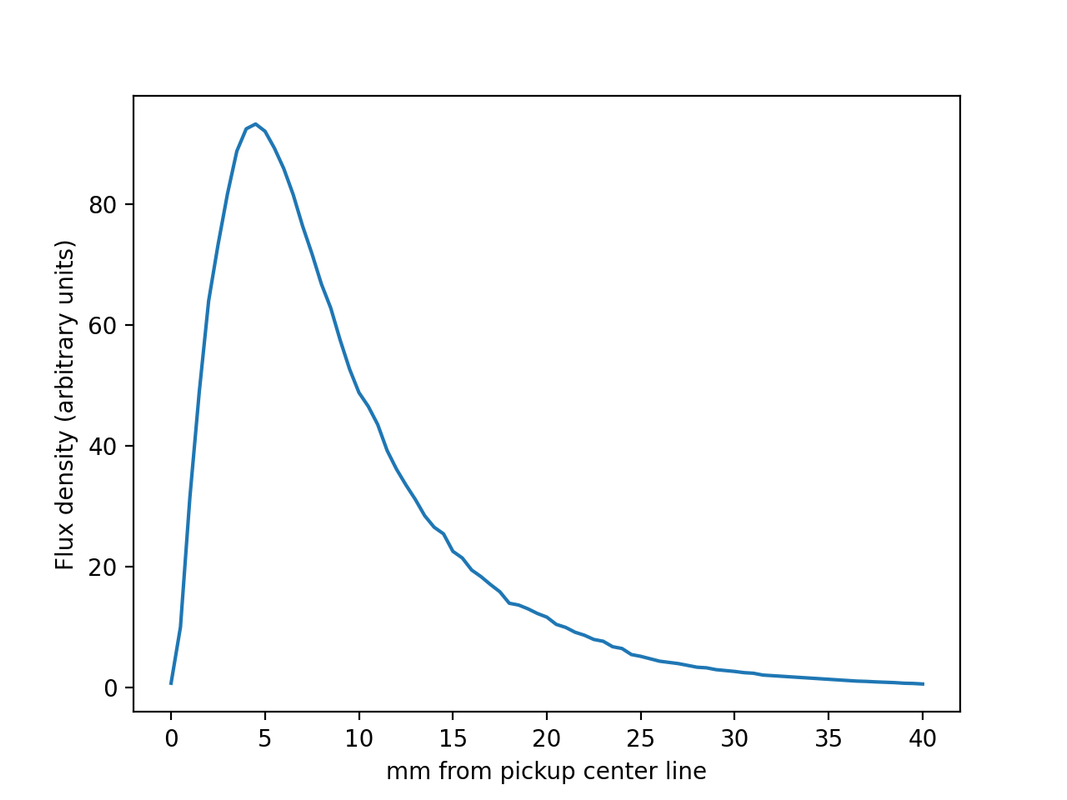This measurement is different from Zollner’s in several important ways. First, Zollner’s measurement is an amazing accomplishment, one that I would have great difficulty duplicating. My measurement is easy; it uses an electromagnet (250 turns #41 AWG around a ferrite core as used in my strat blade pickups to make a field very similar in shape to that of the permanent field from a blade pickup. It is driven with ac (4 KHz, about 8.6 volts peak) rather than dc. This driving field establishes a time varying flux along the string that is sensed with a small coil (10 turns #42 AWG) around the string. The coil is stationary during a measurement (unlike Zollner’s moving coil), but is moved to a number of different locations along the string with a measurement at each.

The signal is about one mv max, and is measured by scope, fft analyzer, and a cross spectrum with the driving signal. The signal to noise ratio is very good. The noise on the plot is a result of errors in locating the sensing coil.

The field is about 50 Gauss at the top of the driver, and so it is much weaker than the field from an Alnico rod. Thus, the results are not much affected by the hysteresis of the high carbon string material and show what happens in a simple case. By comparison Zollner’s results appear “squashed”, probably the result of the magnetization approaching saturation.

This measurement method can be used to study string saturation. A strong permanent magnet placed close to the string moves the string magnetic state along a hysteresis curve. The permeability decreases, and so the measurement signal level decreases. This effect is easily measurable, but I haver not yet made detailed quantitative measurements to find the degree of saturation as a function of magnetic field strength.

The measurement setup uses a guitar, and the neck pickup is replaced with electromagnet. I will post a photo later.

[ms]

Her is a photo of the measurement setup.

[aquin43]

A good result. Instead of modulating the magnetic field (link) you have replaced it entirely with an alternating field. On reflection, the response from modulating the field involves the recoil permeability of both the magnet and the string so the approach you have adopted, by exercising more of the hysteresis loop may well give closer to the true answer. Combining these results with a carefully executed measurement of the response to a moving dipole on the string path would give the pole window shape.

[antigua]

Thanks for doing this experiment. This in interesting info. Do you think that if the string saturates magnetically, that the height of the curve in your plot would be lower? Do you think this aperture profile, especially if saturation were to cause more homogony along the length, can cause comb filtering effects?   

[ms]

May 5, 2022 7:56:49 GMT -5 aquin43 said:

A good result. Instead of modulating the magnetic field (link) you have replaced it entirely with an alternating field. On reflection, the response from modulating the field involves the recoil permeability of both the magnet and the string so the approach you have adopted, by exercising more of the hysteresis loop may well give closer to the true answer. Combining these results with a carefully executed measurement of the response to a moving dipole on the string path would give the pole window shape.

Thanks, this was the simplest measurement that I could think of that would give some useful information.  I think the next step is to look at how much the output decreases when a magnet is brought close.  It appears that this information is needed in the  determination the window shape.

[ms]

May 5, 2022 16:56:43 GMT -5 antigua said:

Thanks for doing this experiment. This in interesting info. Do you think that if the string saturates magnetically, that the height of the curve in your plot would be lower? Do you think this aperture profile, especially if saturation were to cause more homogony along the length, can cause comb filtering effects?   

Thank you for commenting.   Yes, I think that saturation, or even well short of  actual saturation, would tend to flatten the peak of the plot, making it look more  like Zollner's result.  The idea is to put a small permanent magnet of known strength near the string (above it, at a set of measured distances) and check this for various sampled distances along the string.  That is, make a set of measurements like the one in the plot, but with the permanent magnet having moved the magnetic state of the string part way along a hysteresis curve, approaching or reaching saturation at the closest distances.

[aquin43]

Adding flux from an auxiliary magnet will break the symmetry of the magnetisation cycle within the string so the results will depend on the local recoil permeability of the string at the various magnetisations produced by the magnet. I am sure that there would be a flattening of the measured peak but it wouldn't really represent the true flux density.
Surely the best result would come from simply increasing the magnitude of the alternating flux. Getting enough Ampere-turns shouldn't be a problem but the ferrite core would probably have to be replaced by something with a higher saturation flux density. Losses in the core probably wouldn't matter as long as a reasonably sinusoidal flux could be produced. Mechanical vibration of the string might need to be suppressed.

[ms]

May 6, 2022 3:40:14 GMT -5 aquin43 said:

Adding flux from an auxiliary magnet will break the symmetry of the magnetisation cycle within the string so the results will depend on the local recoil permeability of the string at the various magnetisations produced by the magnet. I am sure that there would be a flattening of the measured peak but it wouldn't really represent the true flux density.
Surely the best result would come from simply increasing the magnitude of the alternating flux. Getting enough Ampere-turns shouldn't be a problem but the ferrite core would probably have to be replaced by something with a higher saturation flux density. Losses in the core probably wouldn't matter as long as a reasonably sinusoidal flux could be produced. Mechanical vibration of the string might need to be suppressed.

I agree that the measurements that I propose do not give Zollner's results directly.  Yes, the measurements, when using a small enough drive signal (the measurement sensitivity is very high with proper processing) give the permeability along some B-H curve.  I think that you do a lot with that.

I would also like to try higher drive levels with no biasing field.  The first step is a bobbin that can stand higher temperatures, since PLA is useless for this.  As usual, the limit is heat!  It might not be possible to get a field as strong as  the usual permanent magnet, and I would like to exhaust what I can do with the current coil before trying.

[ms]

What do we observe if we make the “AC magnet” much stronger?

There are several steps in these observations using a much stronger time varying electromagnet magnet:

Preliminary: As described near the end of the first post, locate the tiny string coil where the largest signal is observed using the driving coil described above. Locate a strong magnet above the string and over the driving coil, and observe that with at least several hundred Gauss you can significantly reduce the amplitude of the signal from the string coil. This means that we can move the state of the string along a hysteresis curve to where the permeability is lowered, and so it is worth proceeding with more directed observations.


1. Make a better driving coil; this one also uses a core of #43 material, but it is wound with about 100 turns and has a resistance of about three ohms. It can be driven from an audio amplifier at 400 Hz and delivers about 400 Gauss at the top of the core. 400 Hz is low enough to keep small the inductive effects on the impedance, but high enough to give good sensitivity for sampling and recording with a scope. Heat is the limitation: the coil cannot be excited for more than a couple of seconds without producing a noticeable odor. So far I have not destroyed it. You also have to wait a long time between measurements for the wire to cool. Hot wire has a higher resistivity.
 
2. Check the B field waveform. The first figure shows the waveform of the B field. A sampling coil (the driver coil used earlier repurposed) measures the signal from the driving coil; this signal is digitally sampled, recorded, and read into Python. This signal is proportional to the time derivative of the B field, and so it is integrated to make the signal that has been plotted. This is obviously not a perfect sine wave, probably as a result of effects from the core of the driving coil.   The effect of this distortion can be included in the analysis.l

3. Now measure the signal from the string coil with the new driver coil about 2 mm from the string. The signal from the audio amp is adjusted so that the driver field is about 400 Gauss, measured against the core. (This does not measure the component along the string that excited it, but at least it is proportional to it and provides a reasonable way to character the filed strength.)

4. Process the signal from string coil. This is similar to the processing used to check the waveform fro the driver coil. However, there is an additional step after the integration, and its purpose is to find the hysteresis loop. Thus in the rest of this post we plot and discuss the sampled time derivative of the B field, the integral of this (proportional to the B Field,) and the derived hysteresis loop, presented in arbitrary units. An actual calibration could be done, but for now, the shape of the loop is the issue.

The next figure shows the signal measured by the string coil. It is not even close to a sine wave, suggesting that the field from the driving coil (about 400 Gauss at the peaks of the sine wave) moves the state of the string well into the saturation region. After that we see its integral, a signal proportional to the B Field, and thus the string magnetization. This is closer to a square wave than a sine wave, and thus also suggests saturation.


To make the hysteresis loop we use the the measured integrated B as H  (x axis).  Thus the effect of the distortion due to the driver coil core is included.  The final figure shows the result. As expected, it shows that the driver field continues to increase after the increase in the B field drops sharply.

  

[antigua]

So if you excite with 400G and you see apparent saturation effects in the wave, is it safe to say the guitar string is saturated in situ? And would hysteresis / saturation in a guitar string manifest as a distortion or just a loss in output amplitude? 

[aquin43]

May 21, 2022 20:53:23 GMT -5 antigua said:

So if you excite with 400G and you see apparent saturation effects in the wave, is it safe to say the guitar string is saturated in situ? And would hysteresis / saturation in a guitar string manifest as a distortion or just a loss in output amplitude? 

Surely saturation implies less distortion. The flux returned to the coil depends on the distance of the string from the pole and the degree of magnetisation of the string. In the absence of saturation both of these dependencies would have similarly shaped curvatures that would multiply. Saturation removes or diminishes one of these dependencies.

This is a really useful experiment answering a fundamental question about the state of magnetisation of the string.

I wonder, if the test rig were not a guitar but just something fixed to the bench, could the coil be cooled by immersing most of it in distilled water or light oil?

[ms]

May 21, 2022 20:53:23 GMT -5 antigua said:

So if you excite with 400G and you see apparent saturation effects in the wave, is it safe to say the guitar string is saturated in situ? And would hysteresis / saturation in a guitar string manifest as a distortion or just a loss in output amplitude? 

To add to what aquin43 wrote:  if you make a model of the string magnetization with a pair of long thin permanent magnets, the model is more accurate if the string is saturated.

I should also point out that "400 Gauss" is approximate.  I calibrate by connecting the coil to a dc supply and measuring the B field with a Gauss meter and the voltage across the coil.  Then I measure the peak ac voltage during a measurement with a scope.  It would be better to set up an audio amplifier module as a current source with both ac and dc capability.

[ms]

May 22, 2022 5:46:38 GMT -5 aquin43 said:

May 21, 2022 20:53:23 GMT -5 antigua said:

So if you excite with 400G and you see apparent saturation effects in the wave, is it safe to say the guitar string is saturated in situ? And would hysteresis / saturation in a guitar string manifest as a distortion or just a loss in output amplitude? 

Surely saturation implies less distortion. The flux returned to the coil depends on the distance of the string from the pole and the degree of magnetisation of the string. In the absence of saturation both of these dependencies would have similarly shaped curvatures that would multiply. Saturation removes or diminishes one of these dependencies.

This is a really useful experiment answering a fundamental question about the state of magnetisation of the string.

I wonder, if the test rig were not a guitar but just something fixed to the bench, could the coil be cooled by immersing most of it in distilled water or light oil?

Yes, I think that would work.  The dielectric constant of the cooling medium should not be an issue, I think.  A metal tank would be good for cooling the cooling medium.  You could let it run until it heats to equilibrium, and then it should be stable enough for good measurements.

But for now, I will attempt a set of measurements similar to that shown in the first post, but with the larger field using the current setup.  This will be slow,  but might give some useful information. 

[ms]

Here is the measurement of the magnetic flux along the string for the low field case (blue, same measurement as the first post here) and high field (orange).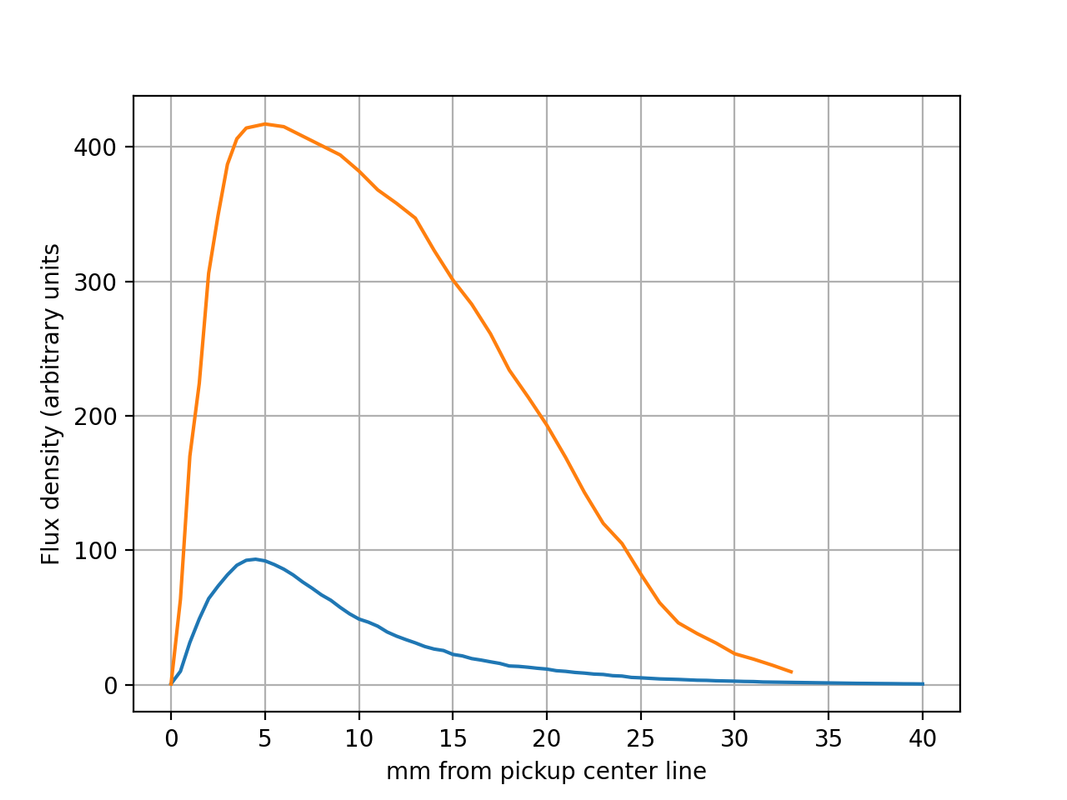




The effects of saturation on the shape of the flux along the string are evident.  The flux is probably underestimated somewhat because the measurement uses only the fundamental of the response. As shown in a previous post, the response in time is a similar to a rounded square wave, and the harmonics are not included in this cross spectral measurement, used because it gives high signal to noise ratio conveniently.
 
Some of the noise in this measurement is undoubtedly the result of variations in temperature increases in the wire in the driver coil (that is, not waiting long enough between measurements). It would be good to improve the setup before making measurements of strings made from different grades of steel for comparison purposes.

[antigua]

Given that PAFs generally show about 1/4th the field strength compared to Fender AlNiCo 5, can you guess as to how likely one is to saturate the guitar string compared to the other, supposing that the pickups are an average distance from the strings, say five millimeters? 

Do you think that this string saturation will cause a slight suppression of higher harmonics, since the magnetic focus essentially becomes wider? 

[ms]

May 31, 2022 11:37:27 GMT -5 antigua said:

Given that PAFs generally show about 1/4th the field strength compared to Fender AlNiCo 5, can you guess as to how likely one is to saturate the guitar string compared to the other, supposing that the pickups are an average distance from the strings, say five millimeters? 

Do you think that this string saturation will cause a slight suppression of higher harmonics, since the magnetic focus essentially becomes wider? 

I think a humbucker located 5 mm from the string (which is a farther than I would  for a bridge pickup, but might be necessary for a neck pickup depending on the height of the action) probably does not get to full saturation. A Fender sc type with A5 does easily, or so it appears.

What we are measuring is the flux pointing along the string in the string.  It is changes in the flux pointing through the coil that induces voltage in the pickup.  These two are related in the following way: Where the flux pointing along the string changes slowly with distance along the string, there is almost no field outside the string.  Where it changes quickly, we do get a field, and that includes a component pointing through the coil.  (Think of replacing the string with two long thin cylinder magnets with like poles nearly touching.)

Now you can see why I put the results of weak and strong field on the same plot.  Both show relatively rapid change near the pole piece, but slow change elsewhere.  So the length of the sampling window does not depend much on whether the string saturates.  (As Zollner pointed out, this is a bit more complicated for a hum bucker if the flux from a pole in one coil extends along the string to the corresponding pole of the other coil.)

[aquin43]

I am trying to relate these results to the flux received by the pickup assembly. On the assumption that the external effect of the magnetisation pattern in the string will be the same no matter how it is originally caused, I repeated my faked up string in FEMM using an array of magnets with linear magnetisation properties to produce a pattern in the string generally similar to the measured ones - in this case more like the unsaturated version. Using the axisymmetric mode in FEMM should give a decent approximation to the 3D situation with axial flux being oriented along the string "x" and radial in what would be the normal "y" direction along the pole axis. The pole space is sketched in as a box. The results are shown in the diagram. I have scaled up the external fluxes by one million relative to the internal peak.

The general shape of the "x" direction flux seems to be a defocused version of the internal flux, while the  radial "y" direction flux peaks over the pole and actually reverses about 7mm out from the centre.

[ms]

That modeling looks really good, and I think the results are close to the actual physical situation.

I think it is possible to use this 2D model to get a reasonable estimate of the voltage generated by a pickup, although it might be a bit of a stretch.  We need the flux change through the coil when the string moves.

1. In the 3D case think of moving  the coil instead of the string.

2. The box on the color plot is a disk with a hole in the middle in 3D.

3.  Consider the change in  flux in the part of the coil closest to the string when the hole size changes.

4. Consider subtracting the integrated flux before and after changing the hole size by a small amount.

5.  This is a short piece of thin walled tubing, a small rectangle in 2D, ignoring the outer rim. 

6. Integrate this flux in the small rectangle.

7. Estimate the fraction of this flux that would pass through the top of a 3D coil.

8. Multiply the result of 6. by this fraction.

9.  Use this value to estimate the flux change in the rest of the coil, using the model results
to determine approximately how fast it falls off.

10. Add it all up.

[aquin43]

I have modified the string to reflect the saturation effect. The curve of the flux in the coil narrows as predicted.

There is enough information in the simulated result to calculate the flux distribution in an air cored coil wound on the imaginary pole piece. Unfortunately there is no way of estimating the effect of the pole piece itself, without which the pickup would be useless.

Without a pole piece, the total flux falls very rapidly with distance from the string. In a 12mm wide coil space, 17mm tall if we take the total flux at 4mm to be 1 then half way down the coil it is 0.13 and at the bottom 0.038 for the saturated string.

For the unsaturated string the results are  1, 0.12, 0.033

[ms]

Pickups using low permeability cores are low output, but they are not useless.  For example, antigua's current discussion is about firebird pickups using a ceramic blade magnet as a core.  He rejects them for their low output, but not everybody does.

(Those looking for a basic discussion including the rule of thumb: hard magnetic materials (permanent magnets) have low permeability, soft magnetic materials (low permanent magnetization) can have high permeability, could look here 
idealmagnetsolutions.com/knowledge-base/magnetic-permeability-table/.  The Wikipedia article on ceramic (ferrite) permanent magnets says they have high permeability.  There are many kinds of ferrite, but I do not believe that that combination is possible.)

Everybody's favorite musical permanent magnet, AlNiCo, has a relative permeability of just a few, and Zollner points out that nearly all the output is generated in the part of the coil nearest to the string in a strat pickup.

Also, I do not see a problem with using the field from your simulation to excite a high permeability pickup core in another simulation.  The potential problem would be that in reality the core magnetization would alter the string magnetization, requiring a complicated self-consistent solution.  However, I think it is much too weak to matter.

[yanyan]

Can the interested but technically deficient audience members get a simplified version?

[veliko]

Guys I wanna start with great work! I am really inspired by your research and doing my best (struggling) to make sense of it all.

What is the ultimate goal of this experiment?

Is it to find the area where we have the highest concentrated flux density and strategically place coils in that area?


aquin43 said:

There is enough information in the simulated result to calculate the flux distribution in an air cored coil wound on the imaginary pole piece. Unfortunately there is no way of estimating the effect of the pole piece itself, without which the pickup would be useless.



Without a pole piece, the total flux falls very rapidly with distance from the string. In a 12mm wide coil space, 17mm tall if we take the total flux at 4mm to be 1 then half way down the coil it is 0.13 and at the bottom 0.038 for the saturated string.

For the unsaturated string the results are 1, 0.12, 0.033

I read the article in magnet permeability table it suggests that neodymium magnets have a permeability that's very close to air, so if polepieces were neodymium you'd be able to to calculate the flux distribution. I dnt know all the implications of a neodymium pole piece (feel free to school me) but I guess if it was that easy you would have done that already.

Which leads me to the question: What is the significance of core permeability and is it desirable?

And the same for string saturation, is it desirable and what's the significance?

[antigua]

Jun 22, 2022 12:53:02 GMT -5 veliko said:

There is enough information in the simulated result to calculate the flux distribution in an air cored coil wound on the imaginary pole piece. Unfortunately there is no way of estimating the effect of the pole piece itself, without which the pickup would be useless.



Without a pole piece, the total flux falls very rapidly with distance from the string. In a 12mm wide coil space, 17mm tall if we take the total flux at 4mm to be 1 then half way down the coil it is 0.13 and at the bottom 0.038 for the saturated string.

For the unsaturated string the results are 1, 0.12, 0.033

I read the article in magnet permeability table it suggests that neodymium magnets have a permeability that's very close to air, so if polepieces were neodymium you'd be able to to calculate the flux distribution. I dnt know all the implications of a neodymium pole piece (feel free to school me) but I guess if it was that easy you would have done that already.

Which leads me to the question: What is the significance of core permeability and is it desirable?

And the same for string saturation, is it desirable and what's the significance?

The pole piece is like an antenna for the coil. The more permeable the pole pieces, the more they will magnetically react to the moving the guitar string, and the more they react, the more voltage you get out of the coil. It extend the magnetic change further down into the coil, so all together you get more flux change when the string moves, and more voltage. 

If the string does not saturate, then it's flux density would rise and fall as the guitar string moves nearer and farther from the magnetized pole piece, but if its saturated at all times, then the flux density in the string stays the same as it moves back and forth. As they said above, when the string is saturated and behaving like a permanent magnet, the output will be more linear and less distorted. Distortion means more harmonics, or more treble, so in summary, if the magnetic field is weak enough to where the guitar string doesn't saturate, you will get a little more treble in the output, but whether that small difference can be heard with your ears or not is another question. A weaker magnetic field also causes less magnetic string pull, less string pull also reduces harmonics (but in the guitar string itself and not as a consequence of distortion), so it's in the end it's a wash, and probably all sounds the same to our ears, but this is more about understanding what is happening, rather than providing actual practical information.