A better treble bleed circuit

[JohnH]

Thanks for the Dr Kev link, and I see he gives me a name check. Cheers Kev!

Dr Kev writes a good summary there. Id add a couple more things about choosing a set of values:

A passive treble bleed can only be a best compromise, though it can be quite a good one. For each system, the best values to suit your wishes are likely to depend on what reduced volume you are targetting. eg, do you mainly want to make a small volume reduction to a clean tone? or a large reduction to clean-up a highly distorted tone? A lower intended volume will tend to favour a smaller cap to maintain a given tone. Worth thinking about as you launch into A/B testing.

Also, all the systems that work have quite a broad range over which different values sound much the same. Having tried a few to help decide what I was going for, I found the analytical approach to finding an optimun helped my engineers OCD mind make a decision, but others will have different opinions.

[newey]

A good summary by Dr. Kev. He does advise that one experiment to determine optimal values for one's particular desires, but then says "it's not so easy" for most people to do that experimentation.

But it's not so tough. One can simply run two wires from the V pot lugs, (the lugs across which one would be wiring the TB circuit) and test various combos external to the guitar. (OK, not so easy on a Strat, but then nothing with wiring ever is on a Strat . . .)

If one has an old 3-way (or 5-way) lever switch lying around, it can be wired as a "cap substitution" switch; wired the two V pot leads to the two poles of the lever switch, then wire 3 test-value cap/resistor combos, or caps alone, across the 1,2, and 3 lugs. Instant A-B-C comparisons can then be done. Once optimal values are found, wire those in permanently and button everything back up.

If done with a 5-way, 5 combos can be A-B'd, but one has to get all mathy to figure out the values for the notch positions.

This has of course been proposed hereabouts before, by ChrisK among others, but a good idea bears repeating. It's a whole lot better than repeatedly soldering/desoldering different combos (and a lot easier on your poor volume pot).

As an aside, I gave a silent "Bravo" to Dr.Kev for his "I'm not discussing it" slam-down take on Bumblebee caps and their ilk.

[benvigil]

I've been looking up the TB values for some signature guitars... two that surprised me: both the Ibanez Vai JEM series and the Joe Satriani JS series use a single 330pF cap for treble bleed.

newey, I have a few Super Switches arriving tomorrow and plan on wiring one up as a 5-way TB tester. It drives me bonkers that I have to re-string or disassemble half the axe just to get the pickguard off. I'm REALLY tempted to route the back of my G&L to give me control access. I'm clearly not sentimental about my guitars.

[JohnH]

I ran the Dimarzio 560pf/330k and Ibanez/PRS 330pF TB circuits through GuitarFreak, to compare to a 150k/1000pF treble bleed:

The plots show an envelope of predicted output (including string and harmonic effects), with all traces normalized for volume so tonal difference is clearer.

In all cases, the initial max-volume tones first loses some treble as you turn down, and then this recovers and eventually increases with more treble.

The dashed blue lines are max volume (Vol 10), and there are three other traces for the greatest deviation below the base case, the greatest deviation above (based on a 3db max difference), and the reduced volume at which the match is best (red). The comparisons are made up to 3500hz, which is just above the electrical resonance peak.

The traces are with two 500k pots (log) a 10' cord and a 6-part model of a DiMarzio PAF Pro, in the bridge position.


DiMarzio 330k//560pF






330pF






150k//1000pF




All three designs work OK, but the 150k/1000pF is a bit more consistent, and definitely is better than the others at controlling the initial treble fall when reducing volume from max,. It also stays within a good range over a wider sweep of the volume knob. But actually, by the time all versions are at the lower limits used above, they are all at a reduction of about the same amount of db, being about -11, -12 and -13 db for the 330pF, 330k//560pF and 150k//1000pF respectively. The different knob sweep is mainly dependent on the way the resistors change the taper, but the 150k//1000pF gives a slightly wider range over a wider sweep.

So its personal choice and 'horses for courses', but I still prefer the 150k/1000pF.

[Deleted]

Works with the Volume POT, 220pF when the Bleed is ON, 820pF on the first stage [Location 10-8 or 7] (820pF+220pF = 1n04F) then Middle stage [7-4ish] another 820pF comes in Series with the first 820pF (Cutting it down to 410pF+220pF=630pF ) before Last Stage [4-1] dropping out and just leaving the 220pF
There is no small CUT that makes it Cackle when it jumps from one to another, its set at a angle so that it can select both parts and not be bothered as one just shorts the other and doesnt mind

[eivar]

Sorry for resurrecting,
In your op, is it correct that if i use a wireless system, i wont be needing a treble bleed?

How about i install a TB and use wireless? Will that increase the effect of TB? Or what will happen?

[reTrEaD]

Hello eivar. to the GuitarNutz family.

No need to worry about resurrecting an informational thread like this one, with a question.

You are correct, when using a wireless, treble-bleed is not necessary (and somewhat undesirable). The purpose of treble-bleed is to mitigate the effect of the cable capacitance and series resistance of the pot in reduced volume setting working together to form a high-cut filter. Since cable capacitance is not present when using a wireless, when you turn down the volume, there will be more high frequency content present than there should be. Your reduced volume setting will sound brighter than it should.

For a guitar which is intended for use exclusively with a wireless, you should omit the treble-bleed.

For a guitar which will be used often with a wireless and often without, a switch would be a handy addition. Or two output jacks. One regular jack and the other with a built-in switch which will disconnect the treble-bleed when a wireless is plugged into it.

[JohnH]

There's a couple more things that can be taken into account too:

Treble bleed has no effect at max volume, it only comes into play at reduced volume. Cable capacitance affects tone at all volumes, but the dulling effect is greater as lower settings of the volume pot, which is what TB compensates for.

Most, or at least many, wireless systems have a switch to add a little capacitance to simulate a cable. I think guitars sound best with about 10' of cable rather than zero capacitance.

So whether you add TB or not, there are a few options and work-arounds possible to find your tone.

[eivar]

Thank you reTrEaD and JohnH for the answers! I guess my wireless setup will be my tone reference for experementing TB network and values. And I guess i may not install TB to one of my guitar that i use usually live with wireless.

[reTrEaD]

Nov 12, 2010 7:11:42 GMT -5 JohnH said:

A no treble bleed
B a treble bleed capacitor
C a treble bleed capacitor in parallel with a resistor
D a new and improved design using a variable parallel resistor, based on a dual gang pot for the volume control

John, I've been looking at the 'Type C' with some interest, trying to discern how it does what it does. Here' my present take on that.

Type A (no treble bleed) suffers from what is essentially a high-cut filter when the volume is reduced from maximum. This filter is comprised of the series resistance of the pot (CW to wiper) and the cable capacitance. The more the volume is reduced (to a point), the more effective the high-cut.

Type B (capacitor only) attempts to compensate for this. It does a somewhat decent job at slightly reduced volume but it overcompensates and does so to an even greater degree the further the volume is reduced.

The parallel resistor in Type C substantially increases the loading (lower resistance) on the pickup as the volume is reduced. This increased loading causes an increasing loss of high frequencies the more the volume is reduced. This tends to work in opposition to the overcompensation of the treble bleed capacitor. The net result is that it tracks reasonably well throughout a wide range of volume settings.

Another side effect is the resistor in the parallel treble bleed network changes the 'law' of the pot. It requires more CCW rotation from maximum to achieve the same amount of attenuation as a volume control with no treble bleed.

---

While this description isn't fully analytical, I think it does help understand the basic mechanism. What do you think?

[JohnH]

Yes I'd agree with all of that. And one has to accept the change in the pot taper, but actually, it comes out to a very nice net result IMO, about 30% at mid turn which gives good control in the upper volume ranges. There are special pots for guitars that have that, for special $, and this system does it by default.

[thetragichero]

was photographing my bc rich mockingbird to list it for sale and apparently i used the JohnH better treble bleed on the neck pickup! i knew i wanted to try it but didn't realize i had

[Yogi B]

May 4, 2020 17:47:10 GMT -5 reTrEaD said:

The parallel resistor in Type C substantially increases the loading (lower resistance) on the pickup as the volume is reduced. This increased loading causes an increasing loss of high frequencies the more the volume is reduced. This tends to work in opposition to the overcompensation of the treble bleed capacitor. The net result is that it tracks reasonably well throughout a wide range of volume settings.

Another side effect is the resistor in the parallel treble bleed network changes the 'law' of the pot. It requires more CCW rotation from maximum to achieve the same amount of attenuation as a volume control with no treble bleed.

I don't know if I saw this at the time it was posted, but I'm seeing it now and I don't think I'd quite say it like that.

Firstly I'd've said the points about loading and the pot's law the other way around: adding the resistor changes the law of the pot, and it is because of this that for a given amount of volume reduction that the loading is increased.

If we take a standard 10% 500k pot at the halfway point of it's rotation, then the pot adds 450k of series resistance and 50k parallel (load) resistance. And the DC output voltage is reduced to a total of 50k / (50k + 450k) = 0.1 of the input voltage.

Adding a 220k tapering resistor to the 'upper' portion of the pot means that in order to get the same reduction in voltage we must to turn the pot further down -- this makes sense, after all we've changed the pots law. Naturally as we turn the pot further the parallel load resistance decreases -- in this specific case it will be around 17k when we achieve 10% voltage.

SPOILER: Click to show

\gdef\k{\textrm{k}}
\gdef\M{\textrm{M}}
\gdef\G{\textrm{G}}

\begin{aligned}
0.1 &= \frac{R}{R + \frac{220\k \cdot (500\k - R)}{220\k + 500\k - R}}
\\[1.5em]
R + \frac{220\k \cdot (500\k - R)}{220\k + 500\k - R} &= 10 R
\\[1.5em]
\frac{220\k \cdot (500\k - R)}{220\k + 500\k - R} &= 9 R
\\[1.5em]
220\k \cdot (500\k - R) &= 9 R (720\k - R)
\\[1.5em]
110\G - 220\k R &= 6480\k R - 9R^2
\\[1.5em]
R^2 - \frac{(6480\k+220\k)R}{9} &= \frac{-110\G}{9}
\\[1.5em]
\left( R - \frac{3350\k}{9} \right)^2 &= \frac{-990\G + 11222.5\G}{81}
\\[1.5em]
R &= \frac{3350\k \pm \sqrt{10232.5\G}}{9}
\\[1.5em]
R &\approx 16.8\k
\\
& \text{or}
\\
&\approx 728\k\text{ (discounted since $R < 500$k)}
\end{aligned}
Sanity Check: \dfrac{16.8\k}{16.8\k + \left( 220\k \parallel (500\k - 16.8\k) \right)}
\approx \dfrac{16.8\k}{16.8\k + 151\k}
\approx 0.1

Secondly, despite that the parallel resistor causes a change in loading which in turn affects the response of the treble-bleed (this being relevant to the following main part of this post), that is not my primary concern when thinking about parallel treble-bleeds. Generally what I do think about is the ratio of DC resistance to the impedance of the capacitor (Z_C). This can be reasoned about using only the numbers that have been calculated thus far -- there's no need to calculate the actual impedance, the only extra piece of information we need to know is that the impedance of a capacitor is inversely proportional to frequency.

For high frequencies (treble) Z_C is small, thus the resistance in parallel with capacitor makes little difference to the total impedance (450\k \parallel Z_C \approx Z_C and 151\k \parallel Z_C \approx Z_C). Whereas for low frequencies (bass) Z_C is large, the resistance is the dominant contributor to the total impedance (450\k \parallel Z_C \approx 450\k and 151\k \parallel Z_C \approx 151\k).

In other words: while both the cap only treble-bleed, and cap & resistor in parallel treble-bleed represent roughly the same impedance for treble frequencies; however, for bass frequencies the impedance of the cap only variant is roughly three times larger than the cap and 220k resistor in parallel variant. (Where lower values of the capacitor itself increase the frequency where the distinction between what are considered bass and treble frequencies -- hence why we tend to see lower valued caps when not combined with a parallel resistor.)

---

Now, on to the actual point of this post...

I've been thinking about the varitone (and thus inductors) quite a lot recently, even before frets' recent transformer acquisition. During which I had an idea, the second instalment of how we can manipulate cable capacitance for our own benefit (following on from a previous thread about a tone control variant).

My thought process is as follows: as noted in reTrEaD's above quote, one consequence of any parallel resistor + capacitor treble-bleed design is extra loading particularly at lower volumes; this extra loading manifesting itself as a lowering and widening of the resonant peak (i.e. lowered Q-factor); adding an extra degree of filtering (e.g. going from a 1st order filter to a 2nd order filter, etc.) is usually paired with increased Q-factor; perhaps, therefore, some variation of treble bleed that more accurately maintains the shape of the resonant peak could be possible via the introduction of an inductor into the mix. Following is my current best attempt to do just that.

As you'll see in the accompanied schematic, if were to venture further down the rabbit hole of over-engineering and diminishing returns, then I might as well start out with "A Better Treble Bleed Circuit" and attempt to make it 'betterer'. In the below plots V(out) represents JohnH's ClearTone volume with 130k resistor and 820pF capacitor, V(out2) represents my new variation as shown in the schematic below -- both versions are based on the same 500k dual gang idealised log pot, a (modern wired) 500k tone pot, 500pF cable capacitance, 1Meg input impedance, and the 3-part Seth Lover Model from GuitarFreak. (I'm guessing this was the model used at the beginning of this thread, the OP specifies "a vintage humbucker" but due to the relatively large resonant peak this appears prior to GF's inclusion of 6-part models. Additionally, since the whole point is that I'm trying to give a better match for the peak, it makes sense to use a model that has a prominent one.)

The first image shows an overlaid sweep of the two variants from 10 down to 1 (using Gibson knob numbering). The two variants are close in overall amplitude, but the narrower peak of the new variant (blue) should be immediately obvious.

The next image shows the same sweeps, however the amplitude of the steps has been corrected such that the DC amplitude of all the plots is equal -- the top plot is the ClearTone. The colouring is as follows: (max volume) 10 - red; 9 - orange; 8 - yellow; 7 - green; 6 - blue; 5 - purple; 4 - dark red; 3 - dark orange; 2 - dark yellow; 1 - dark green.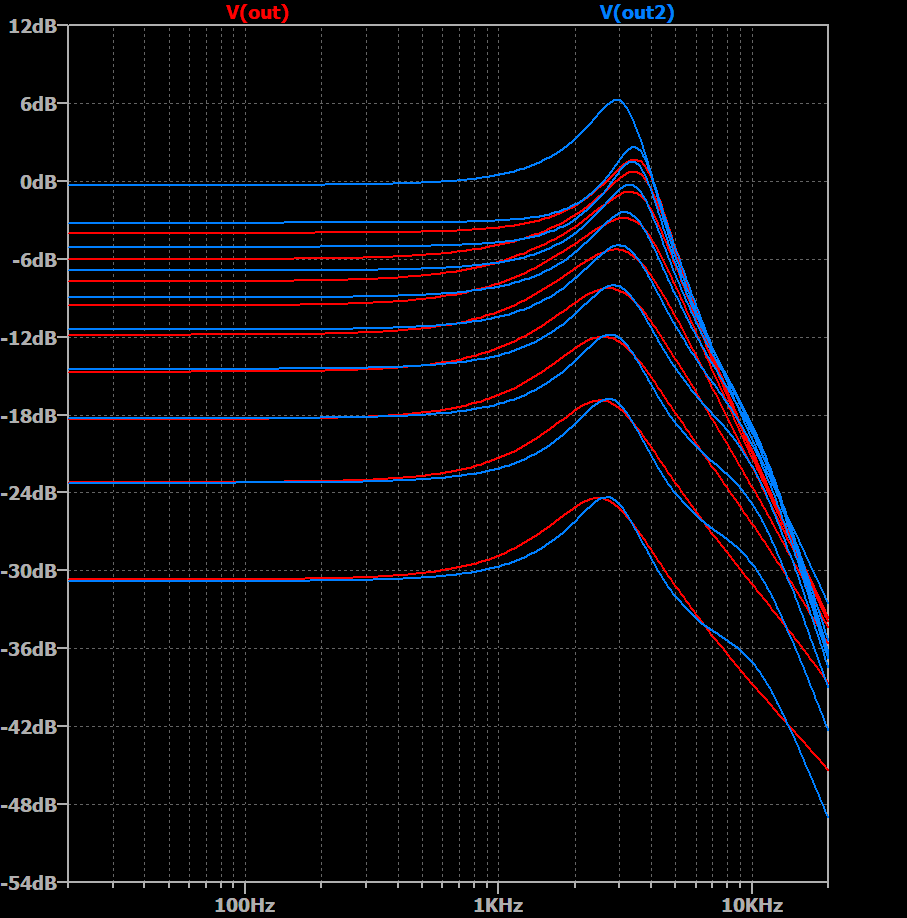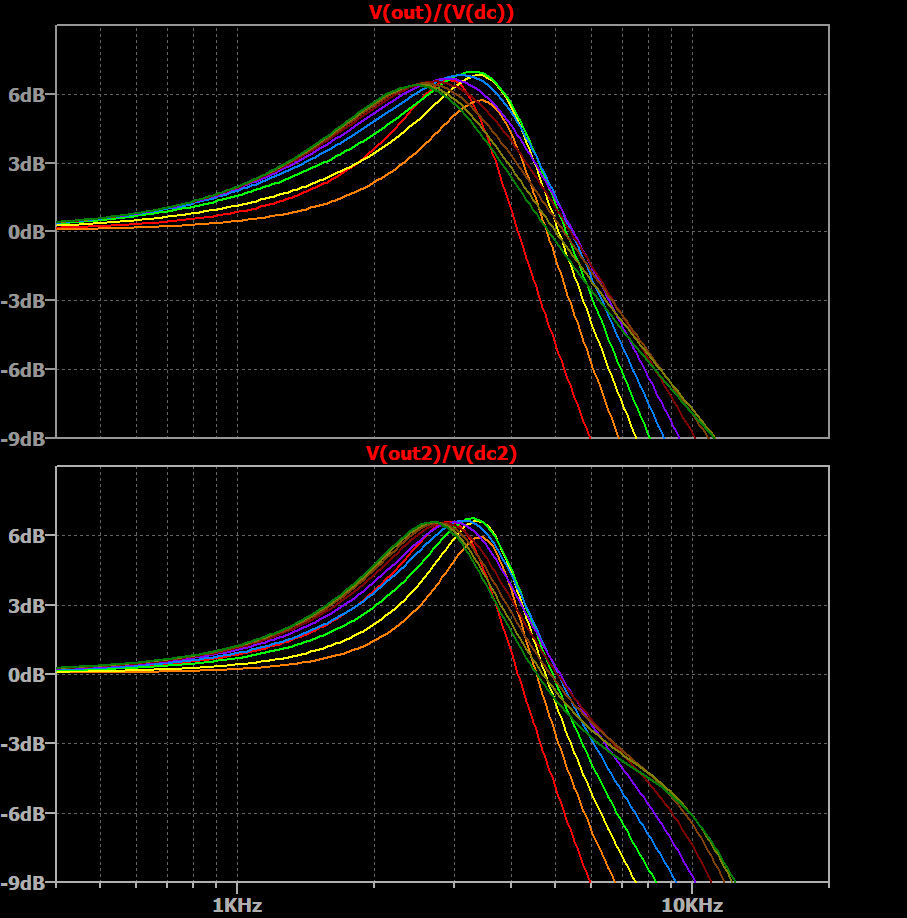



Schematic:

[JohnH]

very nice study!

What i use to judge these things is to normalise volumes at an arbitrary frequency such as 440hz, then subtract in dB's the full volume tone from that of the new candidate. The ideal is zero difference at all frequencies, and I judge a range where max-min deviation is within 3db to be good, and 2db would be better, within a frequency range up to just above the resonant peak.

Are you able to make a few comparisons on that basis? The key places are at about 8.5 or 9, around 5 or 6, and maybe about 3.

The design is improved if the range of deviations is reduced, and or, it stays close within a wider volume range or a wider frequency range.

That inductor in the model, is it typical of the kind of values that frets is using?

And on my earlier studies, yes they used early GuitarFreak versions using 3-part models. It wasn't until we met Antigua that a whole lot of real data was available to deliver better models. But in terms of making conclusions about treble bleed, so long as its apples or its oranges that are being compared, the conclusions don't really seem to change with the better models.

[Yogi B]

Feb 8, 2021 16:21:39 GMT -5 JohnH said:

What I use to judge these things is to normalise volumes at an arbitrary frequency such as 440hz, then subtract in dB's the full volume tone from that of the new candidate. The ideal is zero difference at all frequencies, and I judge a range where max-min deviation is within 3db to be good, and 2db would be better, within a frequency range up to just above the resonant peak.

That's kind of what I was trying to show in the second image, but I know it's a bit busy with all the overlapping traces.

Are you able to make a few comparisons on that basis? The key places are at about 8.5 or 9, around 5 or 6, and maybe about 3.

I can but it isn't half a faff in LTspice.

Getting the amplitude at an arbitrary frequency is possible via a .MEAS(URE) statement, but that outputs to the log file -- and while you can plot that data from there, I'm not aware of a way to combine it with any of the traces from the main plot window. Therefore, one has to copy the textual results from the log file, strip the irrelevant bits in order to reformat it as arguments to LTspice's table function, and use that to specify the voltage for a behavioural voltage source (after converting from dBs back into Volts).

Although not being too much for a one off, it's too much to do repetitively. Therefore I usually end up doing comparisons normalized at 0Hz which is much easier, it's just a case of duplicating the circuit and replacing inductors & caps with shorts & open circuits as appropriate.

The plot below is based on the same as the second of those in my previous post, but has been renormalized at 440Hz and I've divided though by the max volume (red) trace in order to give the dB difference (hence why the red trace is now a straight line at 0dB). Again the ClearTone 130k + 820p is the top plot with the new variation below, and the colours represent the same steps as before.

The design is improved if the range of deviations is reduced, and or, it stays close within a wider volume range or a wider frequency range.

Looking at the above plot the new variation is admittedly worse at 9 & 8 (orange & yellow) so there is definitely room for improvement, but otherwise it remains within ±1dB (up to 3.2kHz, after the peak) between 7 & 2, with 1 being only just outside that range.

That inductor in the model, is it typical of the kind of values that frets is using?

I believe so, or at least it's based on one of the transformers she's previously had: the 42TL018 (see here). The reason I jumped on this now was to see if the suspected low inductance transformers she's just acquired would be suitable, but alas it appears not.

One unknown is the parasitic parallel resistance for these transformers/inductors (i.e. equivalent to the damping/load resistances in the 6-part pickup models). Based on this plot of the response of the BluesHawk's Varitone circuit the parasitic parallel resistance of it's 7.2H inductor seems to be in the region of 250k, something similar in a treble bleed situation would largely nullify the benefit of including the inductor in the first place. Though I'm probably comparing apples & oranges as the BH inductor is a significantly larger value and encased in some unknown metal which may contribute to eddie currents. Additionally there could be some other outside factors that I'm missing as even the plots without the Varitone, just the Blues90 pickup (no dummy coil), lack much of a resonant peak which (even when taking loading from controls & a standard guitar cable into account) is very surprising given they're (purportedly underwound) P90's with AlNiCo rod magnets.

[JohnH]

another thought:

Given the idea of these is to maintain the resonant peak as volume goes down, it might help if the TB has a minimum impedance at the required peak frequency, to let the most through there. This happens when the reactance of L1 is equal and opposite to that of C2, and then the inductor/capacitor branch has an impedance equal to its series resistance.

With the current values, this minimum happens at 4.5kHz. (F = 1/(2pi(LC)^0.5) Increasing C2 could bring this down to 2.8kHz, and maybe add a series resistor.

It would not be too hard to hack GuitarFreak to add the inductor. Then its all in a spreadsheet so easy to wrangle plots etc

[burgher79]

Looking to add a treble bleed to my Guthrie Govan guitar. However, instead of a 500k audio taper pot, I’m planning on using a 500k linear pot, mainly due to it also having a 4pdt switch on it.

The Guthrie Govan Charvel normally has a 500k audio pot with 680pf and 150k treble bleed circuit (Suhr values). I very much liked the more linear effect the circuit gave the volume pot. It is a HSH setup.

How will using a 500k linear pot with the 680pf/150k or 1000pf/150k treble bleed circuits affect the pot taper compared to an audio taper pot?

I suspect that it may mean even less effect on the volume knob between 10 and 5, and push control even further to the bottom end of the volume range, which would not be what I want. If this is the case, is there anything I could do to compensate for this?

I will give it a try with just capacitor to see the effect, then try capacitor and resistor in parallel too.

[JohnH]

Yes indeed, if you start with a linear pot and add a parallel treble bleed, it wil further reduce the effect of turning down volume until you are at low knob settings. The tones available are not affected though, so it'll still work.

You may have to experiment, maybe a higher resistor value such as 270k, or put the cap and resistor in series (see kinman treble bleed, maybe with more cap)

The parallel version was the best simple arrangement just for tone, but you'll find what works best for you in all respects.

[David Mitchell]

Jun 23, 2017 22:08:08 GMT -5 JohnH said:

Its a matter of picking values that keep the tonal range most intact while changing volume. Its a 'best compromise' rather than an absolute, but it works very well. So having tried a few options with testing and analysis, my conclusion is broadly as reTrEaD posted above.

Its not really dependent on the pickups themselves.

It works best for 10' cords. If you use a longer cord, it doesn't really change the optimum values, but the full volume tone then tends to shift to nearer the 10' tone as you roll down, not a bad thing!

The best simple arrangement is a resistor and cap in parallel, and 150k with 1nf works very well. It makes no difference at full volume, and does its best job in the range 5 to 9.

But if your most important low-volume range is less than about 5, a slightly smaller cap is slightly better, say 0.68nF or 0.82nF.

If you use a 250k pot, I suggest the same cap values but reduce the resistor to 120k

The TB circuit slightly reduces the steepness of fall off of the pot taper as you roll down, about half way to being a linear pot - this is also a good thing!

That's about all I know.

Thanks for your expertise again, JohnH! This is such a helpful summary I think it should be appended to your first post. 

Do you know if your standard suggestion (150k and 1nf) would work well with a 1M pot?

Context: I am hoping to install Filtertron-style pickups in my guitar after a while. I read a post on TDPRI by antigua suggesting that 1M pots would be a good choice for them, and then happened across a test of various pots with Filtertrons on YouTube, in which I liked a blend of 500k and 1M. I'm still thinking (contrary to advice) about using a blender pot, so I might pair a 500k blender, 1M volume, and no-load (or modified TBX) tone control.

[JohnH]

I think 150k and 1000pF would still be a good option to try. Id go for 500k volume and 500k no-load blend rather than two 1M pots. No-load is also good for simple blenders, to get them fully off when not blending.

[David Mitchell]

Jan 29, 2022 2:40:13 GMT -5 JohnH said:

I think 150k and 1000pF would still be a good option to try. Id go for 500k volume and 500k no-load blend rather than two 1M pots. No-load is also good for simple blenders, to get them fully off when not blending.

JohnH, thank you again. I left out a detail on the context: The blender I'm thinking of is the Bourns PDB182-GTRB, a dual blender that would replace the pickup selector; which you've advised against, if I recall correctly, but I still want to try.

If you have time, can you explain why you'd advise against 1M pots? Or should I ask somewhere else?

[unreg]

Hi David Mitchell, I just know that the higher rating of the pot used for tone, the more shrill the treble sounds. Maybe that has something to do with JohnH’s 500K pot recommendations over 1meg-ers.


500K is usually used for humbuckers; my humbucker guitar sounds infinitely better with a 250K tone pot. Has too much treble at 500K, for me at least.

[sumgai]

Jan 29, 2022 22:25:20 GMT -5 unreg said:

.... my humbucker guitar sounds infinitely better with a 250K tone pot. Has too much treble at 500K, for me at least.

I'd be interested in seeing the specs on that pickup. Either it's a miraculous unit, or you're somebody who hasn't yet experienced age-related hearing loss. 

[unreg]

Jan 30, 2022 11:48:28 GMT -5 sumgai said:

Jan 29, 2022 22:25:20 GMT -5 unreg said:

.... my humbucker guitar sounds infinitely better with a 250K tone pot. Has too much treble at 500K, for me at least.

I'd be interested in seeing the specs on that pickup. Either it's a miraculous unit, or you're somebody who hasn't yet experienced age-related hearing loss. 

Hmm… my ears have been called pretty good. One of the humbuckers is a blue Dimarzio Bluesbucker. The other one, in the neck position, came with my ESP LTD M-155. (The guitar was made on a Korean assembly line. Though, it works super well now. 🙂)

[MattB]

David Mitchell, I'm also planning a guitar with Filtertrons. I've tried out a few different treble bleed values in JohnH's Guitarfreak spreadsheet, and it  seems like a standard treble bleed doesn't do a great job with Filtertrons for some reason. These plots were made using 500k volume and tone pots, but I did quickly try a 1 meg volume pot with the standard 1nF/150k values, and it didn't look a whole lot different.

Here are 4 different sets of treble bleed values, going from 10 to 1 on a 500k log pot.

And here's the same 4 charts, normalised at 440Hz.

1nF/150k does the best job at high volumes, but overcompensates at low volumes, and the variation between the brightest and darkest sound is in my opinion way too big. 0.82nF/82k does well at low volumes, and has the smallest overall variation, but a little more treble loss between 10 and 9, and it takes longer to brighten up again as the volume is rolled down. 1nF/100k and 0.82nF/100k are probably better all-round options, but they still aren't all that great.

For comparison, here's an equivalent plot made with the SD59 pickup model.

It's not perfect, but the treble bleed does a better job of maintaing a similar overall shape, and the variation is less; around 4dB (EDIT: 5dB) difference in top end between the brightest and darkest sounds, compared to around 8dB for a Filtertron with the same values.

I decided at this point that putting a buffer in the guitar was a better option for me, so it's possible that a different set of values could work better, or at least suit your taste better.

If you haven't already, I would very much recommend trying out Guitarfreak yourself- it's very simple and intuitive, and I have learned a whole lot of useful things from it.

[JohnH]

Nice work getting GF going again!

One or things to bear in mind with the plots:

The more standard HB and SC pickups show a strong peak in response, and so the plots have a wider vertical dB scale, than for the Filtertrons, where their inherent damping gives them a flatter response, hence with a plot in GF that covers a smaller range, graphically expanded vertically. So what looks like a wider deviation may be actually more similar in dB's

The plots, as used there, are all pinned at 440hz. If you release that feature in the small tick-box just above the title, you can see then them in volume relation to each other.

That 150k/1nF recipe is probably working about the same in db terms

The values with much smaller resistors in the TB circuit are also changing the pot taper more

I think with a guitar as unique as those that have these pickups, it definitely will pay to rig up a way to experiment with differed values, and use GF to give some insight to guide the tests, rather than to work out a recipe blind.

My friend has beautiful Gretsch 6120 Brian Setzer model with Filtertrons on it. I've never been able to persuade him that he needs me to rewire it with a treble bleed!

[MattB]

Feb 1, 2022 3:00:50 GMT -5 JohnH said:

One or things to bear in mind with the plots:

The more standard HB and SC pickups show a strong peak in response, and so the plots have a wider vertical dB scale, than for the Filtertrons, where their inherent damping gives them a flatter response, hence with a plot in GF that covers a smaller range, graphically expanded vertically. So what looks like a wider deviation may be actually more similar in dB's

The plots I posted all have the same vertical scale, 2.5dB per division. On checking back I did notice that I made a mistake with the SD59 plots; I didn't notice the tone pot was set to no-load. The corrected version has a little more variation between brightest and darkest sounds, but still less than a Filtertron with the same values. I have replaced the SD59 image in my post with a corrected version.

[JohnH]

How about this as a TB candidate for Filtertrons?




Its a 100k with 0.82nF. It seems to meet the criteria I look for for variations. With the dashed blue being volume 10, and looking at up to 4500hZ, the maximum range of relative tone above or below the reference is within 3db for each trace. The traces are at 10, 9, 8 etc, down to 1.6 on the knob, at which point this test is at 2.99 db range (cell M29 at lower right). I interpret that as, at any knob position, if you took the tone trace and moved it to put it as a best fit over the reference, every frequency could be no more than 1.5db above or 1.5db below.

Definitely there's tone variation here, but it looks like it might be reasonable?. Maybe worth a try and then vary from there.

[David Mitchell]

Jan 31, 2022 14:15:42 GMT -5 MattB said:

David Mitchell, I'm also planning a guitar with Filtertrons. I've tried out a few different treble bleed values in JohnH's Guitarfreak spreadsheet, and it  seems like a standard treble bleed doesn't do a great job with Filtertrons for some reason. These plots were made using 500k volume and tone pots, but I did quickly try a 1 meg volume pot with the standard 1nF/150k values, and it didn't look a whole lot different.

I decided at this point that putting a buffer in the guitar was a better option for me, so it's possible that a different set of values could work better, or at least suit your taste better.

If you haven't already, I would very much recommend trying out Guitarfreak yourself- it's very simple and intuitive, and I have learned a whole lot of useful things from it.

Thanks, MattB, for the feedback! As you've seen, I'm trying to experiment with GuitarFreak now. The buffer idea ... well, I may have to edumacate myself on that now....

Feb 1, 2022 14:44:40 GMT -5 JohnH said:

Its a 100k with 0.82nF. It seems to meet the criteria I look for for variations. With the dashed blue being volume 10, and looking at up to 4500hZ, the maximum range of relative tone above or below the reference is within 3db for each trace. The traces are at 10, 9, 8 etc, down to 1.6 on the knob, at which point this test is at 2.99 db range (cell M29 at lower right). I interpret that as, at any knob position, if you took the tone trace and moved it to put it as a best fit over the reference, every frequency could be no more than 1.5db above or 1.5db below.

Definitely there's tone variation here, but it looks like it might be reasonable?. Maybe worth a try and then vary from there.

Thanks, JohnH! That will be my starting point if I continue with this plan, assuming there are no further refinements.

[carlosg]

Great topic. 
I tried your treble bleed, but I don't like it, it change log pot to like linear. For cleans and crunch it will be good, but on the distortion it works like on off  
I prefer only cap. But 330pF like in Ibanez guitars is too much. 
Prs uses 180pF and it is good, but to sometimes to bright. When i tried with my overwound pafs, good value is between 82-180pF. 
Can you share treble bleed chart with 82pF, 100pF, 120pF, 150pF and 180pF? 
I am very curious what it would look like